O systemach liczbowych

Systemy liczbowe

Literatura:
Turski, Propedeutyka ...; Skomorowski, ...

Dwójkowy system pozycyjny

W dziesiętnym systemie pozycyjnym ciąg cyfr 321.23 oznacza liczbę

3·10²+2·10¹+1·10⁰+2·10^{- 1}+3·10^{- 2}

Jeśli przez b oznaczymy podstawę systemu liczbowego, a cyfry przez d_i to każdą liczbę N, która zawiera n cyfr w części całkowitej i m cyfr w części ułamkowej możemy zapisać w postaci

n - 1
∑
i= - m

d_i b ⁱ

lub w postaci :

N=d_{n - 1}d_{n - 2}... d₀.d_{- 1}d_{- 2}... d_{- m} .

Kropka oddziela część całkowitą i ułamkową. W maszynach cyfrowych używa się układów o podstawie b = 2. Cyframi są tutaj 0 i 1. Liczby należące do różnych systemów zliczania zapisuje się często w nawiasach z indeksem b , np. (10101.0101)₂ W systemie dziesiętnym b = 10. Cyframi są 0, 1, ... 9. W często używanych systemach ósemkowym ( b = 8) i szesnastkowym ( b = 16) cyframi są 0, 1, ... 7 oraz 0, 1, ..., 9, a, b, c, d, e, f odpowiednio. Przykłady: (123.45)₈=1·8²+2·8¹+3·8⁰+4·8^{- 1}+5·8^{- 2}=84.578125. (c3.af)₁₆=12·16¹+3·16⁰+10·16^{- 1}+15·16^{- 2}=196.5625 Aby dokonać zamiany liczby dziesiętnej na liczbę o podstawie b należy ją najpierw podzielić na część całkowitą i ułamkową i dokonać zamiany poszczególnych części. Zamianę części całkowitej wykonujemy dzieląc ją kolejno przez podstawę systemu beta i zbierając kolejne reszty z dzielenia w porządku "z prawa na lewo". Zamiany ułamka właściwego dokonujemy mnożąc go przez podstawę b i biorąc z wyniku część całkowitą. Następnie, po odrzuceniu części całkowitej proces powtarzamy (mnożenie, zapamiętanie części całkowitej wyniku, odrzucenie jej), aż do chwili gdy w wyniku dostaniemy jedynkę lub gdy uzyskamy wymaganą dokładność.

Przykład. Zamienimy 35 na liczbę dwójkową.

35/2=17r1 ,17/2=8r1 ,8/2=4r0 ,4/2=2r0 ,2/2=1r0 ,1/2=0r1 .

Mamy więc:

(35)₁₀=(100011)₂

Przykład. Zamienimy 0.90625 na ułamek dwójkowy.

0.90625×2 = 1.8125→1

0.81250×2 = 1.6250→1

0.65000×2 = 1.2500→1

0.35000×2 = 0.5000→0

0.50000×2 = 1.0000→1

Wynik

(0.90625)₁₀=(0.11101)₂

Przykład. Zamienimy liczbę (321.123)₁₀ na liczbę ósemkową. Ponieważ

(321)₁₀=(501)₈ ,

(0.123)₁₀=(0.144)₈ ,

(321.123)₁₀=(501.144)₈ .

Zauważmy, że skończoność rozwinięcia dziesiętnego nie pociąga skończoności np. rozwinięcia dwójkowego. Przykład: 7/20=(010110100...)₂. Liczby dwójkowe łatwo jest zamieniać na liczby ósemkowe (i szesnastkowe). W tym celu należy liczbę podzielić na grupy trzy (cztero) bitowe w lewo i w prawo od kropki dziesiętnej i zastąpić otrzymane grupy cyframi dziesiętnymi (szesnastkowymi).

Przykład.

(100100111100111.1010101)₂

(100 100 111 100 111 . 101 010 1)₂ = (44747.521)₈

(100 1001 1110 0111 . 1010 101)₁₆=(49e7.a5)₁₆

Kody uzupełnieniowe

Uzupełnień używa się w układach cyfrowych do przedstawiania liczb ujemnych. Upraszcza to operację odejmowania. W każdym systemie zliczania o bazie b mamy dwa sposoby uzupełniania.

uzupełnianie do ( b - 1)
uzupełnianie do b

1 Uzupełnienie do b - 1. Uzupełnienie n-cyfrowej liczby N o podstawie b do ( b - 1) jest zdefiniowane jako

( b ⁿ - 1) - N.

W przypadku liczb dziesiętnych ( b - 1)=9, a dla dwójkowych 1.

Przykład. Uzupełnieniem liczby (53412)₁₀ do 9 jest

( b ⁿ - 1) - N=(10⁵ - 1) - 53412=46587 .

Przykład. Uzupełnieniem do 1 liczby (1010101)₂ jest

( b ⁿ - 1) - N=(2⁷)₁₀ - 1 - (1010101)₂=(128 - 1 - 85)₁₀=(42)₁₀=(101010)₂ .

Uzupełnienie liczby do 1 w systemie dwójkowym dostaje się przez odjęcie każdej jej cyfry od 1. Liczbę otrzymaną w ten sposób można też otrzymać przez zanegowanie wszystkich cyfr liczby (―0 = 1, ―1 = 0).

Przykład. Uzupełnieniem do 1 liczby (11001110101)₂ jest (110001010)₂. 2 Uzupełnienie do b . Drugim rodzajem uzupełnienia n-cyfrowej liczby N jest uzupełnienie do b. Jest ono zdefiniowane jako

b ⁿ - N

Można to tez zapisać w postaci

b ⁿ - N=[( b ⁿ - 1) - N]+1

Można je więc otrzymać przez dodanie 1 do uzupełnienia liczby do ( b - 1). Uzupełnienie liczby dwójkowej można otrzymać następująco: idąc od lewej strony liczby pozostawiamy wszystkie zera i pierwszą jedynkę bez zmiany i negujemy następne cyfry.

Przykład. W liczbie (100011010101)₂ pozostawiamy 1000 bez zmian i negujemy 11010101. Otrzymamy uzupełnienie liczby równe (100000101010)₂. 3 Odeljmowanie w systemie o podstawie b . Odejmowanie M - N. Jeśli liczby są bez znaku odejmowanie możemy wykonać następująco:

Do odjemnej M dodajemy uzupełnienie do b odjemnika N

M+( b ⁿ - N)=M - N+ b ⁿ.
Jeśli M ≥ N to w ostatnim wyrażeniu pomijamy b ⁿ, otrzymując w wyniku M - N.
Jeśli M < N to wyrażenie z 1) można zapisać w postaci

M+( b ⁿ - N) = b ⁿ - (N - M)

Jest to uzupełnienie do b różnicy (N - M). Biorąc uzupełnienie do b i mnożąc je przez -1 otrzymamy

( - 1){ b ⁿ - [ b ⁿ - (N - M)]}= - (N - M)=M - N .

Zadanie 1: Odejmowanie 1. Odjąć, pokazaną metodą, liczby M=(1999)₁₀ i (1948)₁₀.

Zadanie 2: Odejmowanie 2. Odjąć M=1999 i N=1999.

Zadanie 3: Odejmowanie 3. Odjąć M=(1948)₁₀ i N=(1999)₁₀.

Zadanie 4: Odejmowanie 4. W powyższych zadaniach zamienić liczby dziesiętne na dwójkowe i wykonać następnie ich odejmowanie metodą uzupełnień.

Dwójkowe liczby ze znakiem

Znak liczby dwójkowej można reprezentować pisząc 0 (plus, +) lub 1 (minus,-) na początku liczby. n-bitowa liczba dwójkowa ze znakiem może być wobec tego przedstawiona za pomocą n+1 bitów. Liczby dwójkowe ze znakiem dają się więc przedstawić następująco

znak-moduł (lub znak-moduł prosty)
znak-uzupełnienie do 1 (lub znak-moduł odwrotny)
znak-uzupełnienie do 2 (lub kod uzupełnieniowy)

Zadanie 5: Reprezentacje liczbowe. Wypisać wszystkie liczby 4-bitowe ze znakiem w reprezentacjach znak-moduł, znak-uzupełnienie do 1, znak-uzupełnienie do 2. Zaletą zapisu znak-uzupełnienie do 2 jest to, że zero ma jednego reprezentanta. W kodowaniu znak-moduł lub znak-uzupełnienie do 1, zero ma podwójną reprezentację.

Zadanie 6: Zero. Wypisz reprezentantów zera dla kodów znak-moduł, znak-uzupełnienie do 1 i znak-uzupełnienie do 2. Jeśli przy dodawaniu n-bitowych liczb (dodatnich lub ujemnych) wynik jest liczbą (n+1)-bitową to nazywamy to przepełnieniem (overflow) lub nadmiarem.

Sprzęt liczący

Tranzystor

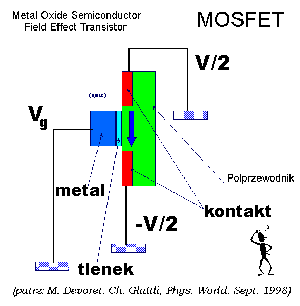
Podstawowymi elementami współczesnych komputerów są tranzystory. Pierwszy tranzystor zbudowali John Bardeen i William Shapley w 1949 roku. Obecnie używane tranzystory różnią się od tych pierwszych pod wieloma względami. Są bardzo małe. Na jednym milimetrze kwadratowym powierzchni można zmieścić kilkaset tysięcy tranzystorów typu MOSFET (Metal Oxide Semiconductor Field Effect Tranzistor). Tranzystor taki zbudowany jest z materiałów półprzewodnikowych napylonych na specjalnej płytce. Schemat budowy tranzystora MOSFET pokazany jest na rysunku.

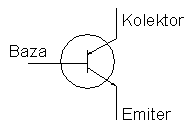
Tranzystor oznacza się często tak jak to pokazuje poniższy rysunek. Strzałki wskazują kierunek prądu. Jeśli napięcie na bazie "rośnie" to sygnał z tranzystora jest większy, jeśli maleje - mniejszy. Ta prosta zależność między sygnałami pozwala na budowę bardziej złożonych układów logicznych, z których składa się komputer.

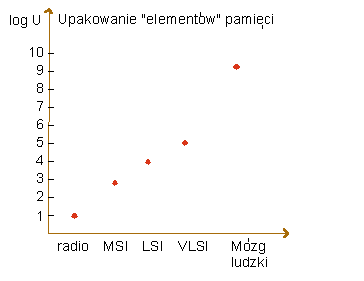
By lepiej wyobrazić sobie jak gęsto upakowane są elementy procesorów i pamięci współczesnych komputerów porównajmy upakowanie różnych ważnych systemów złożonych, zarówno elektronicznych jak i naturalnych, takich jak radio, komputer i mózg ludzki. Daleko jeszcze komputerowym VLSI do natury.

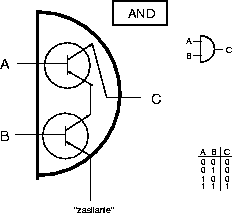
Najprostsze układy elektroniczne noszą nazwę bramek logicznych. Jedną z nich jest bramka AND. Dodaje ona logicznie dwie cyfry binarne: zera lub jedynki. Jej schematyczną budowę i wyniki działania pokazuje następny rysunek.

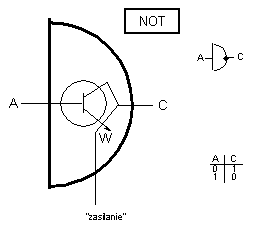
Inną, bardzo prostą bramką logiczną jest NOT - urządzenie negujące. Brak sygnału na wejściu A (baza tranzystora) powoduje pojawienie się sygnały w C, natomiast jego obecność na A powoduje, że prąd ze źródła zasilania płynie bezpośrednio do C - jest sygnał wyjściowy (patrz rysunek).

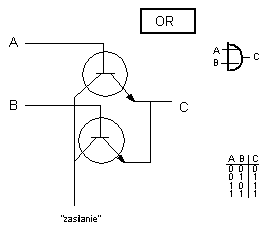
W podobny sposób buduje się inne bramki logiczne, np. OR, NOR, XOR itp.

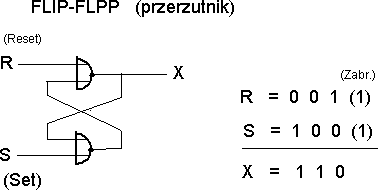
Bramki logiczne odpowiednio połączone tworzą bardziej skomplikowane i użyteczne układy logiczne. Przykładem może służyć tzw. przełącznik flip flop, przerzutnik. Jest to element, z którego budowane są pamięci komputerów. Jego schemat przedstawia następny rysunek. Użyta została tutaj bramka NOR.

Zadanie 7: Schemat NOR. Narysuj schemat bramki NOR używając symbolu tranzystora.

Sumator

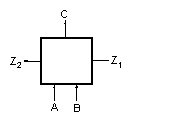
Prostym układem elektronicznym realizującym dodawanie jest tak zwany sumator. Jego schemat można przedstawić następująco.

Przez wejścia A, B i Z₁ do układu docierają sygnały elektryczne - impulsy, które przekształcane są w impulsy na wyjściach C i Z₂. W tabeli podsumowano wyniki jego pracy (1 - impuls, 0 - brak impulsu).

A	B	Z₁	C	Z₂
0	0	0	0	0

0	0	1	1	0
0	1	0	1	0
1	0	0	1	0

1	1	0	0	1
1	0	1	0	1
0	1	1	0	1

1	1	1	1	1

Jeśli a, b i z są jednobitowymi liczbami dwójkowymi to doprowadzając do wejść A, B i Z₁ impulsy odpowiadające tym liczbom, na wyjściu C otrzymamy liczbę dwójkową

c=a+b+z - (10)₂z′

gdzie

z′=

⎧
⎪
⎨
⎪
⎩

gdy a+b+z < (10)₂

w przeciwnym razie.

⎫
⎪
⎬
⎪
⎭

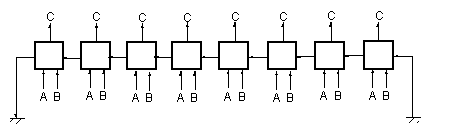
Widzimy więc, że sumator dodaje liczby a, b, z modulo 2. Wynik podaje na wyjście C, a na wyjście Z₂ podaje przeniesienie "w lewo". Jeśli a+b+z ≥ 2 to z′=1 w przeciwnym razie z′=0. Odpowiednio połączone sumatory jednopozycyjne tworzą tzw. sumator wielopozycyjny "bez przeniesienia" lub "z przeniesieniem" (patrz rysunek). Sumatory tego typu mogą wykonywać operacje dodawania liczb n-bitowych. Jeśli np. na wejście sumatora podane będą odpowiednio zakodowane ułamki właściwe to na jego wyjściu pojawi się ich zakodowana suma. 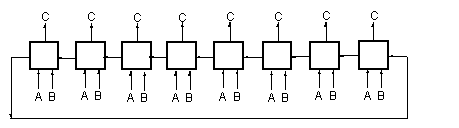Rysunki przedstawiają sumator wielopozycyjny bez przeniesienia oraz sumator wielopozycyjny z przeniesieniem

Arytmometr

W celu wykonania innych działań niż dodawanie używa się wyspecjalizowanych układów logicznych. Składają się one na tzw. arytmometr maszyny liczącej. Prócz układów liczących komputery posiadają w arytmometrze inne układy, tzw. układy pamiętające - rejestry. Rejestry wraz z arytmometrem tworzą tzw. akumulator Dowolne ciągi operacji arytmetycznych takich jak +, -, *, / mogą być realizowane w akumulatorze procesora. Innym ważnym elementem komputera jest pamięć, gdzie przechowuje się dane. Ciągi sygnałów (0, 1) pamiętane są w ciągach komórek pamięci. Sygnały te są ciągle odświeżane. Można je pobierać i zapisywać, a następnie przekształcać w akumulatorze, realizując w ten sposób obliczenia.

File translated from T_EX by T_TH, version 4.03.
On 16 Oct 2013, 21:50.