Elementy programowania komputerów
Program wykładu
- Elementy procesu programowania (definiowanie problemu, szkic rozwiązania, wybór i reprezentacja algorytmu, kodowanie, testowanie i usuwanie błędów, dokumentacja, konserwowanie programów)
- Język potoczny a języki programowania (instrukcja podstawiania, składnia, instrukcje proste i złożone, instrukcje warunkowe, selekcje, schematy: blokowy i Nassiego-Schneidermanna)
- Arytmetyka komputerowa i jej osobliwości (systemy zliczania, komputerowa reprezentacja liczb, działania na reprezentantach, błędy obliczeń i ich propagacja; Przykłady)
- Wprowadzenie do budowy elektronicznych układów obliczeniowych (tranzystor MOSFET, bramki logiczne AND, OR, NOT itp, układy liczące: sumatory)
- Wybrane algorytmy (działania na macierzach, sortowanie tablic, wielomiany, pierwiastki równań algebraicznych).
- Złożoność algorytmów i ich optymalizacja
- Języki programowania ze szczególnym uwzględnieniem Pascal-a (C++, Fortran).
- Struktury danych.
- Elementy programowania obiektowego (pojęcie klasy lub obiektu, dziedziczenie, procedury wirtualne, obciążanie operatorów)
- Obliczenia symboliczne (Mathematica, Maple, Macsyma)
- Historia obliczeń i komputerów
- Gospodarowanie zasobami komputerowymi
- Ciekawostki ze świata komputerów
- Obliczenia równoległe i rozproszone
- Automaty komórkowe, sieci neuronowe, algorytmy genetyczne
- Logiki wielowartościowe i rozmyte
ROCZNICE 50 lat temu, 40 lat temu
1948-9 Claude Shannon: praca o teorii informacji1949 John Bardeen, William Shapley: Tranzystor
1959 Feynman: There is a plenty room at the bottom, Wykład o tzw. Nanotechnologii, 29.XII.1959, CALTECH.
Punkt zaczepienia. Prosty problem.
Na wstępie zdefiniujemy to czego będzie dotyczyć wykład Elementy programowania komputerów, który mam prowadzić dla Państwa. Zastanówmy sie na początku jak obliczamy pierwiastki kwadratowe z liczb dodatnich. Ten prosty problem i jego rozwiązanie, które wszyscy znamy, pozwoli nam poczynić pewne uogólnienia i pozwoli dostrzec wszystkie problemy występujące w tzw. programowaniu, o którym będziemy mówić. Kiedy już je dostrzeżemy i zauważymy ich ważność poświęcimy kilka chwil każdemu z nich by potem łatwiej i lepiej móc pisać programy dla siebie i, co może ważniejsze, dla innych, którzy będą je u Was zamawiać. Zadanie jakie sobie stawiamy brzmi następująco. Dla zadanej liczby dodatniej obliczyć na komputerze (oczywiście bez używania kalkulatora) pierwiastek kwadratowy. Co musimy zrobić? Wczytać dane, tę jedną liczbę a i wydrukować wartość √a. Jeśli jest to liczba kwadratowa, tzn. taka, że jej pierwiastek jest liczbą wymierną to sprawa jest w miarę prosta. Co zrobić jednak jeśli liczbą tą jest 2? Pierwiastkiem jest liczba niewymierna. Jak ją przedstawić? Ile miejsc znaczących wydrukować? Jeszcze inaczej, z jaką dokładnością należy ją policzyć? Sześć? Czy dokładność innych obliczeń zależnych od tak wyliczonego √a (jeśli takie obliczenia prowadzimy) będzie wtedy wystarczająca? Itd, itp. Pytań tego typu będzie jeszcze więcej. Musimy na nie odpowiadać gdyż tego wymaga klient, który zamówił u nas program do obliczeń. Jeśli jest to np. bank lub szpital to konsekwencje złych przybliżeń mogą być fatalne w skutkach. Załóżmy tymczasem, że wiemy już, że dokładność ma wynosić ±10−6, czyli jedna milionowa. Oznacza to, że wynik jaki dostaniemy może sią różnić od dokładnego o wielkość ϵ = 0.000001. Pojawia się wtedy następny problem jak policzyć ten pierwiastek z taką dokładnością. Żeby nie tracić za wiele czasu spójrzmy na poniższy rysunek.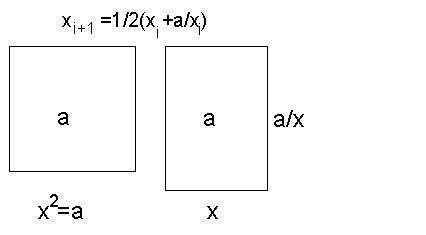
|
|
1: ustal dokładność obliczeń epsilon;
2: wczytaj liczbę a;
3: oblicz pierwiastek z liczby a wg wzoru Herona;
4: drukuj pierwiastek;
To jest prawdziwy schemat. Spróbujmy go udokładnić. Jak potraktować
przypadek ujemnych a? Musimy wczytać nową liczbę a, informując
jednocześnie użytkownika o tym, że wprowadził złą daną.
Programowanie to przewidywanie różnych sytuacji, które mogą się
zdarzyć podczas pracy programu. Lepszy nieco schemat programu może być
następujący.
1: ustal dokładność obliczeń:
epsilon <- 0.000001;
2: wczytaj liczbę a;
jeśli a<0 wykonaj [
wypisz "a jest mniejsze od 0";
idź do kroku 2
];
3: oblicz pierwiastek z liczby a wg wzoru Herona;
4: drukuj pierwiastek;
Schemat powoli rozrasta się. Zajmijmy się teraz krokiem 6.
Powinniśmy ustalić x, obliczyć a/x, obliczyć średnią
xi=1/2(x+a/s) i powtarzać ten proces, podstawiając pod
x nową wartość xi aż do
momentu gdy osiągniemy żądaną dokładność.
1: ustal dokładność obliczeń:
epsilon <- 0.000001;
2: wczytaj liczbę a;
jeśli a<0 wykonaj [
wypisz "a jest mniejsze od 0";
idź do kroku 2;
];
3: ustal x: x <- a/4; { przyjmujemy startowe x=a/4}
I: [
xi <- x; { przechowujemy x również w xi }
x <- 1/2 (xi+a/xi); { wyliczamy nowe "x" }
jeśli abs(xi-x) > epsilon idź do kroku I;
]
4: drukuj pierwiastek wg wzorca zgodnego
z zadaną dokładnością;
Używamy tutaj zdań zdań rozkazujących lub ich równoważników:
rozkazów. Pojawiły się również
rozkazy złożone z kilku linii tekstu - instrukcje złożone,
które zawarłem w nawiasy kwadratowe [...], etykiety, które są
nazwami kroków, pewne funkcje znane w systemie operacyjnym,
tzw. funkcje biblioteczne, np. abs, itd.
W zasadzie można przystąpić do kodowania.
Należy więc wybrać język wyższego poziomu, w którym to
kodowanie przeprowadzimy i przełożyć nasz schematyczny program
na ten język. Czy to koniec? Rozstrzygnięcie jakiego języka
programowania należy użyć nie jest proste. Są ich napewno dziesiątki,
a może i setki.
Dla przykładu podaję Państwu kod problemu wraz z krótkim opisem oraz
przykładem obliczeń, wykonanych w języku Pascal.
program heron; (* DOBRA nazwa dla naszego problemu *)
uses dos, crt; (* dolaczanie bibliotek *)
(*
KOMENTARZ:
Program uzywa algorytmu Herona dla znajdowania pierwiastka
kwadratowego z liczby z dokladnoscia zadana przez uzytkownika.
Jest to metoda iteracyjna, ktora sprowadza sie do wzoru:
x_i = 1/2 * (x+a/x),
gdzie x jest wartoscia poczatkowa, przypuszczalna wartoscia
pierwiastka, ktora moze byc podana przez uzytkownika lub, najlepiej,
obliczona wstepnie w programie.
Powyzszy wzor mozna latwo zrozumiec analizujac nastepujacy rysunek.
(a - pole, x_i - bok, x_(i+1) - drugi bok)
+ - - - - - - - +
. .
. .
. a . x_i = a/x
. .
. .
. .
+ - - - - - - - +
x
Wartosc pierwiastka lezy gdzies pomiedzy x_i i x_(i+1), a wiec jest
rowna 1/2(x_+x_(i+1))=1/2(x_i+a/x_i).
Liczba (a) wczytywana jest z terminala.
Dokladnosc obliczen (eps) jest ustalona przez programiste.
*)
const
eps=1e-9; (* dokladnosc obliczen; blad *)
var
x, xi, a: extended; (* duze liczby! *)
iter: integer; (* gospodarka zasobami pamieci *)
begin
clrscr;
(*
wczytywanie danych:
*)
writeln('Program: HERON');
writeln('Obliczanie pierwiastka kwadratowego z liczby dodatniej.');
repeat
{ czytanie danych i sprawdzanie ich poprawnosci }
write('Prosze podac liczbe (>0): a= ');
until a>=0;
read(a);
if a=0 then
begin
writeln;
writeln('Pierwiastek=', '0');
halt;
end;
(*
obliczenia
*)
time0:=time;
iter:=0;
x:=a/4;
repeat
xi:=x;
x:=0.5*(xi+a/xi);
iter:=iter+1;
until abs(xi-x) < eps;
(*
wypisywanie wynikow:
Dobrej informacji nigdy za wiele!
*)
writeln;
writeln('Liczba: a = ',a:25:9);
writeln('Pierwiastek: x = ',xi:25:9,' +/-',eps);
writeln('Liczba iteracji: iter = ',iter:25);
writeln('Sprawdzenie: x^2 = ',xi*xi:25:9);
writeln('Czas obliczen = ',time-time0:25:9,' sec.');
end.
(* Przykladowe wyniki obliczen. ---------------------------- Turbo Pascal Version 7.0 Copyright (c) 1983,92 Borland International Program: HERON Obliczanie pierwiastka kwadratowego z liczby dodatniej. Prosze podac liczbe (>0): a= 12345678987654321 Liczba: a = 12345678987654321.000000000 Pierwiastek: x = 111111111.000000000 +/- 1.00000000000000E-0009 Liczba iteracji: iter = 30 Sprawdzenie: x^2 = 12345678987654321.000000000 Czas obliczen = 0.000000000 sec. ------------------------------------------------------------------------------ Co mozna dodac do programu? Np. licznik czasu. *)Schemat słowny progarmu możemy zastąpić schematem graficznym, tzw. schematem blokowym.
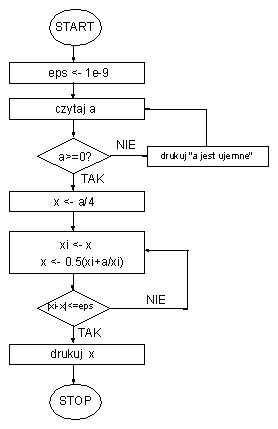
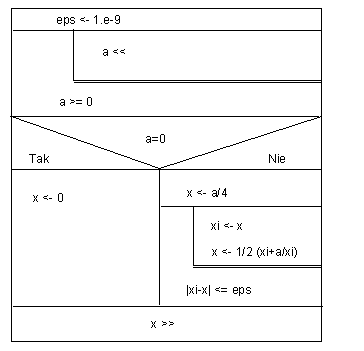
- definicja problemu
- stałe (np. ϵ lub eps (const)
- zmienne (np. x, xi) (var)
- dane i ich typy (type)
- instrukcja przypisania, podstawiania (<-, :=)
- instrukcje warunkowe (jeśli to zrób to;; if ... then),
- instrukcja czytania danych (read, readln)
- instrukcja drukowania danych (write, writeln)
- proces iteracyjny
- dokumentacja, komentarze (patrz prawo Eaglesona, niżej)
- funkcje biblioteczne, biblioteki funkcji i procedur (dos, crt)
- pamięć
- dokładność obliczeń, błędy obliczeń
- algorytm, algorytm skończony
- kodowanie
- języki programowania komputerów
- usuwanie błędów, odpluskwianie (debuging)
Poprawka do prawa Eaglesona, tym razem innego autorstwa brzmi:Any code of your own that you haven't looked at for six or more months, might as well been written by someone else.
Trud włożony w zrozumienie tej prawdy pomoże nam uniknąć wielu rozczarowań. Pamiętajmy o tym pisząc nasze, nawet takie proste jak omawiany tutaj, programy.Eagleson is an optimist, the real number is more like three weeks.
References
- []
- W.M. Turski: Propedeutyka informatyki, PWN, Warszawa, 1989.
- []
- N. Wirth: Algorytmy + struktury danych = programy, WNT, Warszawa, 1989.
- []
- Ś. Ząbek, Elementy programowania komputerów, UMCS, 1994.
- []
- G. Michael Schneider, Steven W. Weingart, David M. Perlman, Programming and problem solving with Pascal, John Wiley & Sons, New York, 1982.
- []
- Cormen, Leiserson, Rivest, Wprowadzenie do algorytmów, WNT, Warszawa, 1997.
- []
- D. E. Knuth, Algorithms, Sci. Am. 236 63-80, (1977).
- []
- D.E. Knuth, Mathematics and computer science: coping with finiteness, Science, 194, 1235-1242 (1976).
- []
- M. Davis, Czym jest obliczanie, w zbiorze "Matematyka współczesna, 12 esejów", red. Lynn Artur Steen, WNT, Warszawa, 1983.
- []
- J. Bielecki, Turbo Pascal, WKŁ, Warszawa, 1989.
- []
- R.K. Kott, Programowanie w języku Pascal, WNT, Warszawa.
- []
- Lo, Y.M.D., Jui, K.F.C., Wong, S.L. Letter. Science 268.28 (April 1995):481.
- []
- M. Sysło, "Trylogia", Warszawa, 1997.
- []
- Robert Ligonniére, Prehistoria i historia komputerów, Ossolineum, Wrocław, 1992.
- []
- Czasopisma komputerowe
File translated from TEX by TTH, version 4.03.
On 16 Oct 2013, 21:50.

