Kompozycje algorytmiczne

Literatura:
Ś. Ząbek, Elementy programowania komputerów . Rozdział 2.

Język potoczny ze swoimi zdaniami rozkazującymi: prostymi i złożonymi może służyć do opisu algorytmów. W zdaniu rozkazującym najważniejsze jest orzeczenie, którym jest najczęściej czasownik użyty w trybie rozkazującym w drugiej osobie liczby pojedynczej. Orzeczenie określa konkretne działanie: przynieś, połóż, zamknij itd. W dalszej części zdanie rozkazujące wskazuje na jakie przedmioty rozciąga się działanie, np. przynieś książkę, a następnie wskazuje ono miejsca umieszczenia przedmiotów, np. połóż książkę na stole. To proste rozumowanie pokazuje, że zdania rozkazujące charakteryzują się następującymi własnościami:
  1. określenie czynności - OPERACJA
  2. wskazanie przedmiotów, których operacja dotyczy - OPERANDÓW
  3. określenie miejsca, w którym umieszcza się wynik operacji
Mamy więc: OPERACJA(operand1, operand2, ...) → Miejsce przeznaczenia. lub Miejsce przeznaczenia := Operacja(operand1, operand2, ...).

Przykład. 

      10! -->  silnia
        x := 2*Pi*R
Operacja := nosi nazwę operacji przypisania. Często używać będziemy tzw. wyrażeń, które same w sobie nie są operacjami w powyższym sensie. Np. wyrażenie (a+b)//2 nie jest instrukcją. Nie wskazano tu miejsca gdzie należy umieścić wynik. Tego typu wyrażenia stosuje się w różnych złożeniach. Są one częścią instrukcji. W językach programowania komputerów zdania rozkazujące zastępuje się odpowiednimi kompozycjami czy konstrukcjami, które służą do wyrażanie intencji programisty i są jednocześnie łatwa do przekładu na język zrozumiały dla maszyny, a więc na kod zero-jedynkowy. Wrócimy do tego problemu później. Tymczasem, wiedząc, że takie języki programowania istnieją, omówimy te konstrukcje albo kompozycje algorytmiczne. Podobieństwo z językiem potocznym nie jest tu przypadkowe. Są one wzięte prawie wprost z języka potocznego.

Złożone zdania rozkazujące - kompozycje.

1 Kompozycja sekwencyjna

Zdanie rozkazujące, a następnie Zdanie rozkazujące
Złożeniu ä następnie" odpowiada w wielu jązykach programowania znak średnika: ; lub znak nowej linii.

2 Kompozycja synchroniczna

Zdanie rozkazujące 1, i równocześnie Zdanie rozkazujące 2
Tego typu konstrukcje używane są w tzw programowaniu równoległym, gdzie obliczenia przebiegają w tym samym (w przybliżeniu) czasie.

3 Kompozycje warunkowe

(dwu- i jedno-wariantowe).
Jeśli Zdanie oznajmujące, wówczas Zdanie rozkazujące 1, w przeciwnym razie Zdanie rozkazujące 2. Ta kompozycja daje możliwość rozgałęzień w algorytmach. Często zdarza się, że drugi wariant jest pusty, np. zdanie "jeśli pada deszcz wówczas weź parasol" zawiera tylko jedno zdanie rozkazujące.

4 Kompozycje wielowariantowe

Pozwalają one na wybór jednego wariantu z wielu możliwych. Najczęściej można je sprowadzić do kompozycji dwuwariantowych.

5 Kompozycja iteracyjna

dopóki Zdanie oznajmujące dopóty Zdanie rozkazujące
Jeśli przez W reprezentować będziemy zdanie oznajmujące występujące w tej konstrukcji, tzw. warunek, a przez R oznaczymy zdanie rozkazujące, to możemy napisać następującą równoważność: dopóki W dopóty R ≡ w razie gdy W, wówczas [ R, a następnie dopóki W dopóty R]. Nawiasy funkcyjne [], w których umieszczamy kompozycji, zawierają znów kompozycję "dopóki, dopóty", powtarzają ją. Tego typu powtarzalność operacji nosi nazwę iteracji. Jest to tzw. pętla dopóki dopóty. W którymś kolejnym kroku wykonywania tego typu poleceń warunek W musi się zmienić tak by pętla została przerwana. Inaczej, wykonywałaby się ona w nieskończoność!

6 Kompozycja iteracyjna aż do

powtarzając: zdanie rozkazujące aż do chwili gdy stwierdzicz, że zdanie oznajmujące
Mamy tu następującą równoważność:
powtarzając: R aż do chwili gdy W ≡ R, a następnie dopóki nie W dopóty R.
Widzimy, że warunek W sprawdzany jest w tej kompozycji po wykonaniu R. Różnicę z kompozycją "dopóki, dopóty" polega na tym, że tam warunek był sprawdzany na początku kompozycji. Jest wiele sytuacji gdzie i jedna i druga kompozycja mają zastosowanie.

7 Kompozycje zagnieżdżone

Ponieważ zdania rozkazujące mogą być zdaniami złożonymi to ich wielokrotne złożenie prowadzi często do tzw. zagnieżdżania kompozycji (jedna w drugiej).

8 Zdania proceduralne

Pobudka! nie jest rozkazem, który można spełnić wykonując jedną czynność. Na jej wykonanie składają się takie czynności jak przebudzenie się, wstanie, słanie łóżka, itp. Każda z czynności cząstkowych jest też złożoną czynnością. Tego typu zawołanie, w programowaniu, nosi nazwę zdania proceduralnego. Np. ObliczPierwiastekKwadratowy określa ciąg czynności obliczeniowych, których wynikiem jest taka liczba, że jej kwadrat jest równy liczbie danej.

9 Konstrukcje rekurencyjne

Przykład (Ząbek):
Obierz n ziemniaków =
      w razie gdy n > 0, wówczas
      [
         weź ziemniak
         obierz ziemniak
         Obierz n−1 ziemniaków
      ]
Tutaj n jest parametrem równym, np. 15. Przykładem rachunkowym może służyć obliczanie silni z liczby n. 
  Oblicz n!"  =
     w razie gdy n=0 za wynik przyjmij 1
     w przeciwnym razie Oblicz (n-1)! i pomnóż ten wynik przez n
Należy zdawać sprawę z różnic pomiędzy konstrukcjami iteracyjnymi i kompozycją rekurencyjną. Za wygodę stosowania rekurencji płaci się często dużym zużyciem pamięci komputera!

Schematy Nassi-Schneidermana

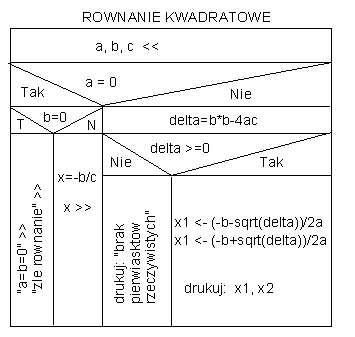
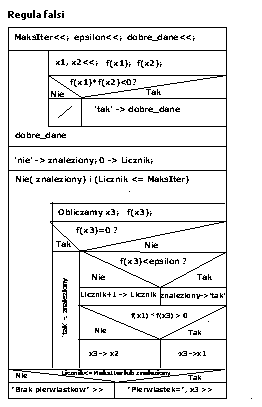
Algorytmy można pisać w języku potocznym. Widzieliśmy to poprzednio w przypadku algorytmu znajdowania pierwiastka metodą Herona. Widzieliśmy też, że zapis taki często bywa mało przejrzysty. Zagnieżdżone zdania rozkazujące, które umieszczamy w opisach, stają sią zawiłe, skomplikowane i mało czytelne. Wystarcza często niewielki schematyczny rysunek, czy diagram by obraz algorytmu stał się jasny. Do przedstawiania algorytmów na diagramach służa tzw. schematy blokowe, podobne do schematów działania urządzeń elektronicznych (telewizor) oraz tzw. schematy Nassi-Schneidermana (N-S). Te ostatnie są mniej szczegółowe, ale za to pokazują wprost główne idee algorytmu. Ukazują, jak mówimy, strukturę algorytmu. Opiszemy je bardzo krótko. Jako przykład pokażę Państwu diagram Nassi-Schneidermana rozwiązywania problemu znajdowania pierwiastków rzeczywistych równania kwadratowego
a x2+b x+ c = 0 .
Zadanie polega na wczytaniu trzech liczb a, b i c oraz wydrukowanie rozwiązań x1 i x2 tego równania jeśli są one rzeczywiste. W przypadku gdy wyróżnik równania kwadratowego jest ujemny należy podać tę informację. W przypadku gdy a=b=0 należy podać informację, że równanie jest złe.
pict//rkwad.gif
Każde zdanie rozkazujące przedstawione jest na schematach N-S za pomocą "klatki", tzn. prostokąta zawierającego to zdanie lub jego skróconą postać. Postać skrócona może zawierać symbole podstawiania (:= lub ->) oraz inne umowne znaki. Jeśli zdanie reprezentowane taką klatką jest złożone, to wnętrze prostokąta dzieli się na figury o różnym znaczeniu odpowiadające opisywanej sytuacji. Zilustrujemy to za chwilę. W przypadku, gdy podział danego prostokąta staje się trudny z powodu jego małych rozmiarów, nazywamy go i rysujemy większy prostokąt o tej samej nazwie, i w nim zapisujemy resztę algorytmu.

W razie, gdy W wówczas R1, w przeciwnym razie R2

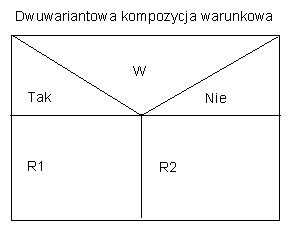
pict//ite.gif
Złożone zdanie warunkowe (konstrukcja wariantowa) W razie, gdy W wówczas R1, w przeciwnym razie R2 reprezentujemy pokazanym wyżej schematem NS.
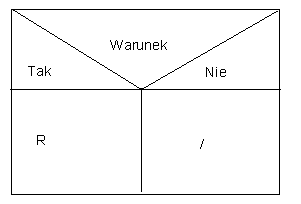
Tutaj W oznacza pewien warunek, zaś R1 i R2 są instrukcjami, z których wykonuje się tylko jedna w zależności od spełnienia warunku W. Całkiem podobnie można reprezentować konstrukcję w razie, gdy W, która nie posiada drugiej części w przeciwnym razie. Prostokąt reprezentujący zdanie rozkazujące z nagłówkiem "N" jest tu przekreślony.
pict//it.gif

dopóki W, dopóty R

Jest to tzw. kompozycja iteracyjna. Spełnienie sią warunku W powoduje powtórzenie refrenu R. Jeśli za którymś razem warunek W nie będzie spełniony refren zostanie pominięty i wykonana zostanie instrukcja, która następuje bezpośrednio po nim. Na schemacie "w klatce W" umieszcza się w prawym dolnym rogu "klatkę R" (patrz rysunek).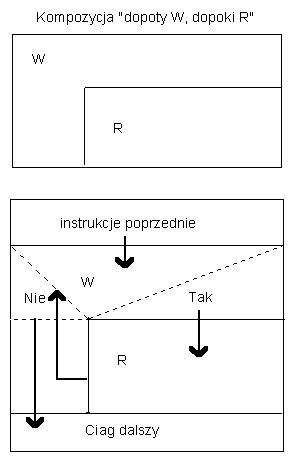
pict//dd.gif
Prawie w każdym przypadku konstrukcji "dopóki-dopóty" występuje wstępne postępowanie P, zwane preludium.

aż do

Konstrukcję powtarzając R, aż do chwili, gdy stwierdzisz, że W można przedstawić w postaci następującej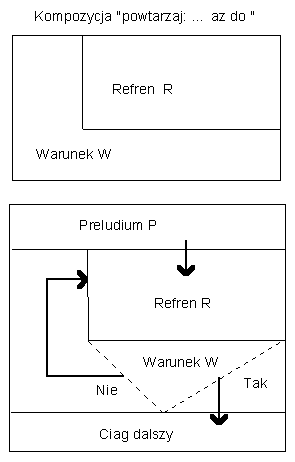
pict//pad.gif
Refren jest zapisany najpierw, a warunek zapisany jest w lewym dolnym rogu schematu. Refren wykonywany jest z powtórzeniami, aż do chwili gdy warunek W zostanie spełniony. Tak jak i poprzednie schematy tak i ten, poprzedzony jest innymi częściami algorytmu. Po nim następuje ciąg dalszy.
pict//falsi.gif

Zadanie 1: Kompozycje. Podaj po trzy przykłady każdej kompozycji algorytmicznej omówionej na wykładzie.

Zadanie 2: Przepis kucharski. Opisz ciąg czynności, który można zastąpić jakimś zdaniem proceduralnym (np. przepis kucharski).

Zadanie 3: Sortowanie 1. Dane wejściowe: Ciąg n liczb <a1, a2, ... an>.
Wynik: Permutacja (zmiana uporządkowania) <a′1, a′2, ... a′n> taka, że a′1 ≤ a′2 ≤ , ... ≤ a′n.
Algorytm: Sortowanie przez wstawianie.

Zadanie 4: Sortowanie 2. Wykonać przykład sortowania przez wstawianie dla ciągów liczbowych: a) A=<5, 2, 4, 6, 1, 3> b) A=<31, 41, 59, 26, 41, 58>.

Zadanie 5: Wyszukiwanie. Dane wejściowe: Ciąg n liczb <a1, a2, ... an> i wartość v.
Wynik: Wskaźnik i taki, że v=A[i] lub NIL jeśli v nie należy do A. taka, że a′1 ≤ a′2 ≤ , ... ≤ a′n.
Algorytm: Napisać algorytm wyszukiwania liniowego, który przegląda ciąg A od strony lewej do prawej, szukając v.

Zadanie 6: Schematy NS. Narysuj schematy N-S algorytmów z poprzednich zadań.

File translated from TEX by TTH, version 4.03.
On 16 Oct 2013, 21:50.