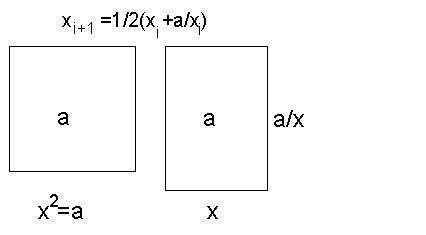Prosty problem
Na wstępie zdefiniujemy to czego będzie dotyczyć wykład
Elementy programowania komputerów, który mam prowadzić dla
Państwa.
Zastanówmy sie na początku jak obliczamy pierwiastki kwadratowe z liczb
dodatnich. Ten prosty problem i jego rozwiązanie, które wszyscy znamy,
pozwoli nam poczynić pewne uogólnienia i pozwoli dostrzec wszystkie
problemy występujące w tzw. programowaniu, o którym będziemy mówić.
Kiedy już je dostrzeżemy i zauważymy ich ważność poświęcimy
kilka chwil każdemu z nich by potem łatwiej i lepiej móc pisać
programy dla siebie i, co może ważniejsze, dla innych, którzy
będą je u Was zamawiać.
Zadanie jakie sobie stawiamy brzmi następująco.
Dla zadanej liczby dodatniej obliczyć na komputerze (oczywiście bez używania
kalkulatora) pierwiastek kwadratowy.
Co musimy zrobić? Wczytać dane, tę jedną liczbę a i wydrukować
wartość √a. Jeśli jest to liczba kwadratowa, tzn. taka, że jej
pierwiastek jest liczbą wymierną to sprawa jest w miarę prosta. Co
zrobić jednak jeśli liczbą tą jest 2? Pierwiastkiem jest liczba
niewymierna. Jak ją przedstawić? Ile miejsc znaczących wydrukować?
Jeszcze inaczej, z jaką dokładnością należy ją policzyć? Sześć?
Czy dokładność innych obliczeń zależnych od tak wyliczonego √a
(jeśli takie obliczenia prowadzimy) będzie wtedy wystarczająca? Itd,
itp. Pytań tego typu będzie jeszcze więcej. Musimy na nie odpowiadać
gdyż tego wymaga klient, który zamówił u nas program do obliczeń?
Jeśli jest to np. bank lub szpital to konsekwencje złych przybliżeń
mogą być fatalne w skutkach.
Załóżmy jednak, że wiemy już, że dokładność ma wynosić ±10−6,
czyli jedna milionowa. Oznacza to, że wynik jaki dostaniemy może sią
różnić od dokładnego o wielkość ϵ = 0.000001. Pojawia się wtedy
następny problem jak policzyć ten pierwiastek z taką dokładnością.
Żeby nie tracić za wiele czasu spójrzmy na poniższy rysunek.
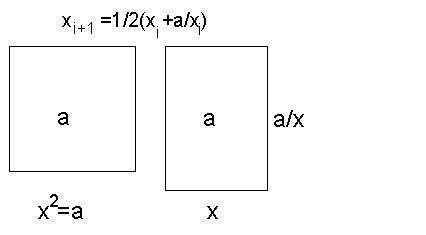
Figure 1: Wzór Herona.
Algorytm obliczania pierwiastka jest natychmiastowy! wystarczy liczyć
średnią wartość z dwóch liczb: jednej x dowolnej (mniejszej od
zadanej liczby a) i drugiej równej drugiemu bokowi a/x. Na
początku, przy zadanym x, liczba a/x jest inna niż x, ale jeśli
będziemy dostatecznie długo powtarzać proces obliczania średniej to
obie liczby będą do siebie dążyć i w nieskończoności iteracji
(tak nazywamy ten sposób powtarzania obliczeń) otrzymamy
Proszę to sprawdzić. Przy pewnym i=i0 będzie
spełniona relacja
. W tym
momencie możemy przerwać proces rachunkowy. Bez tego warunku nasz
algorytm byłby nieskończony. Proces obliczeń nigdy by się nie
zatrzymał.
Mamy więc algorytm obliczeń. Jest to tzw. wzór
Herona1, znany Państwu. Był używany w
szkole. Co najważniejsze, mamy tu algorytm skończony, a więc
proces obliczeń możemy w odpowiednim miejscu przerwać.
Po obliczeniu √a drukujemy wynik z dokładnością zadaną przez
klienta. Dokładnie jednak nie wiadomo co drukować. Tak jest. Czy
drukować sam pierwiastek, czy liczbę i pierwiastek, czy może również
wydrukować dokładność, a może też należałoby w jakiś sposób pozwolić
ustalać dokładność w trakcie rachowania? Okazuje się, że na te
pytania też musimy odpowiedzieć. Musimy te problemy przedyskutować z
klientem. To wszystko należy do tzw. definicji problemu. To nie
jest już tylko obliczenie pierwiastka, ale obliczenie pierwiastka z
zadaną dokładnością i sposób jego przedstawienia.
Komputer pracuje stosując tzw. arytmetykę dyskretną, tzn. używa on
tylko skończonego zbioru liczb co wynika z jego budowy. Każda komórka
pamięci komputera, obojętnie jak duża, może zmieścić próćz tego jakąś
liczbę maksymalną i żadnej większej. Jeśli użyjemy większej liczby
takich komórek pamięci to możemy używać większych liczb. Wynika stąd,
że klient, który zamówił u nas program liczenia pierwiastka powinien
dodatkowo określić jak wielkie liczby kwadratowe będą go
interesowały. To pozwoli nam zdefiniować wielkość komórek pamięci, w
których będziemy zapisywać wyniki obliczeń. Komórki pamięci są podobne
pod tym względem do szuflady: większa szuflada (typ) więcej gratów
(danych) można tam upchać. Można oczywiście używać maksymalnych
dostępnych komórek, ale czasami prowadzi to do zagracenia
pamięci. Niektóre problemy nie wymagają by zmuszać naszego klienta do
zakupu dodatkowych modułów pamięci do jego komputera. Byłby to
nonsens.
Czy już rozwiązaliśmy wszystkie problemy? Jeszcze nie. Musimy naszkicować
projekt programu. Schemat ten nie będzie jeszcze programem dla komputera, ale
pomoże nam wtedy gdy zechcemy taki program napisać. Jak on wygląda?
Np. tak
1: ustal dokładność obliczeń epsilon;
2: wczytaj liczbę a;
3: oblicz pierwiastek z liczby a wg wzoru Herona;
4: drukuj pierwiastek;
To jest prawdziwy schemat. Spróbujmy go udokładnić. Jak potraktować
przypadek ujemnych a? Musimy wczytać nową liczbę a, informując
jednocześnie użytkownika o tym, że wprowadził złą daną.
Programowanie to przewidywanie różnych sytuacji, które mogą się
zdarzyć podczas pracy programu.
1: ustal dokładność obliczeń:
epsilon <- 0.000001;
2: wczytaj liczbę a;
jeśli a<0 wykonaj [
wypisz "a jest mniejsze od 0";
idź do kroku 2
];
3: oblicz pierwiastek z liczby a wg wzoru Herona;
4: drukuj pierwiastek;
Schemat rozrasta się. Zajmijmy się teraz krokiem 6. Powinniśmy ustalić
x, obliczyć aź, obliczyć średnią xi1/2(x+aź) i powtarzać ten
proces, podstawiając pod x nową wartość xi aż do momentu gdy
osiągniemy pas dokładności.
1: ustal dokładność obliczeń:
epsilon <- 0.000001;
2: wczytaj liczbę a;
jeśli a<0 wykonaj [
wypisz "a jest mniejsze od 0";
idź do kroku 2;
];
3: ustal x: x <- a/4 { przyjmujemy startowe x=a/4}
I: [
xi <- 1/2(x+aź);
jeśli abs(xi-x) > epsilon idź do kroku I;
]
4: drukuj pierwiastek wg wzorca zgodnego
z zadaną dokładnością;
Używamy zdań rozkazujących: rozkazów. Pojawiły się również
rozkazy złożone z kilku linii tekstu - instrukcje złożone,
które zawarłem w nawiasy kwadratowe [...], etykiety, które są
nazwami kroków, pewne funkcje znane w systemie, funkcje
biblioteczne, np. abs, itd.
W zasadzie można przystąpić do kodowania.
Należy więc wybrać język wyższego poziomu, w którym to
kodowanie przeprowadzimy i przełożyć nasz schematyczny program
na ten język. Czy to koniec? Rozstrzygnięcie jakiego języka
programowania należy użyć nie jest proste. Są ich setki.
Dla przykładu podaję Państwu kod problemu wraz z krótkim opisem oraz
przykładem obliczeń, dokonanych w Pascalu.
program heron;
uses dos, crt; { dolaczanie bibliotek }
{
KOMENTARZ:
Program uzywa algorytmu Herona dla znajdowania pierwiastka
kwadratowego z liczby z dokladnoscia zadana przez uzytkownika.
Jest to metoda iteracyjna, ktora sprowadza sie do wzoru:
x_i+1 = 1/2 * (xi+a/źi)
gdzie xi jest wartoscia poczatkowa, ktora moze byc podana przez
uzytkownika lub, najlepiej, obliczona wstepnie w programie.
Powyzszy wzor mozna latwo zrozumiec analizujac nastepujacy rysunek.
(a - pole, x_i - bok, x_(i+1) - drugi bok)
---------------
| |
| |
| a | x_(i+1)=a/ź
| |
| |
| |
---------------
x_i
Wartosc pierwiastka lezy gdzies pomiedzy xi i x_(i+1), a wiec jest
rowna 1/2(x_+x_(i+1))=1/2(x_i+a/ź_i).
Liczba (a) wczytywana jest z terminala.
Dokladnosc obliczen (eps) jest ustalona przez programiste.
}
function time:real; { funkcja pobierania czasu w sec.}
var
hour, minute, second, Hundreds: word;
begin
GetTime(hour, minute, second, hundreds);
{wykorzystanie bibliotek}
time:=3600*hour+60*minute+(second+hundreds/100);
end;
const
eps=1e-9; { dokladnosc obliczen; blad }
var
xi, xi1, a: extended; { duze liczby! }
iter: integer; { gospodarka zasobami pamieci }
time0: real;
begin
clrscr;
{
wczytywanie danych:
}
writeln('Program: HERON');
writeln('Obliczanie pierwiastka kwadratowego z liczby >0.');
repeat
write('Prosze podac liczbe (>0): a= ');
until a>=0;
read(a);
{
sprawdzanie poprawnosci danych:
}
if a=0 then
begin
writeln;
writeln('Pierwiastek=', '0');
halt;
end;
{
obliczenia
}
time0:=time;
iter:=0;
xi:=a/4;
repeat
xi1:=0.5*(xi+a/xi);
xi:=a/xi1;
iter:=iter+1;
until abs(xi-xi1)<eps;
{
wypisywanie wynikow:
Dobrej informacji nigdy za wiele!
}
writeln;
writeln('Liczba: a = ',a:25:9);
writeln('Pierwiastek: x = ',xi:25:9,' +/-',eps);
writeln('Liczba iteracji: iter = ',iter:25);
writeln('Sprawdzenie: x^2 = ',xi*xi:25:9);
writeln('Czas obliczen = ',time-time0:25:9,' sec.');
end.
Przykladowe wyniki obliczen.
----------------------------
Turbo Pascal Version 7.0 Copyright (c) 1983,92 Borland
Program: HERON
Obliczanie pierwiastka kwadratowego z liczby dodatniej.
Prosze podac liczbe (>0): a= 12345678987654321
Liczba: a = 12345678987654321.000000
Pierwiastek: x = 111111111.000000000 +/- 1.00000000E-0009
Liczba iteracji: iter = 30
Sprawdzenie: x^2 = 12345678987654321.000000000
Czas obliczen = 0.000000000 sec.
------------------------------------------------------------------
Co mozna dodac do programu? Np. licznik czasu.
Czego nauczyliśmy się z tego przykładu? Jest to tamat na następny
wykład. Możemy tylko powiedzieć, że zdefiniowaliśmy wiele
problemów, których na pierwszy rzut oka nie widać, a które zawsze
występują w procesie programowania. O nich będą te wykłady.
Footnotes:
1Heron z Aleksandrii (stgr. Heron ho
Aleksandreus, ok. 10 - 70) – starożytny grecki matematyk, fizyk,
mechanik, wynalazca i konstruktor.
File translated from
TEX
by
TTH,
version 4.03.
On 16 Oct 2013, 21:50.