Przykład: REGULA FALSI

Literatura:
Schneider, Weingart, Perlman, Programming ..., Wiley, 1982.

Zajmiemy się teraz problemem znajdowania miejsc zerowych jakiejś funkcji f(x). Jest to bardzo stary i ważny problem matematyczny. Miejsce zerowe funkcji f(x) albo pierwiastek równania f(x)=0, to taki punkt x* w którym f(x*) jest zerem. Przykładem funkcji f(x) może być chociażby sin3(x)−x2.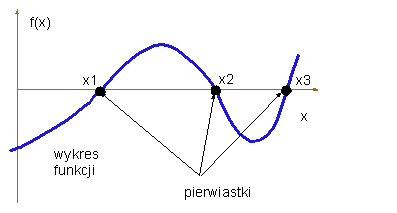
pict/regfal1.gif
W celu znalezienia pierwiastków będziemy korzystać z metody zwanej regula falsi (złego położenia). Nie jest to najlepszy algorytm i na pewno można znaleźć wiele lepszych od niego, ale dla naszego celu, którym jest nauka procesu budowy programu ta metoda jest w sam raz. Poszukiwanie pierwiastka zaczyna się od tego, że mamy najpierw dwa punkty, które obramowują pierwiastek, tzn. mamy takie wartości x1 i x2, że f(x1) i f(x2) mają przeciwne znaki. Załóżmy że wygląda to tak jak na rysunku.
pict/regfal2.gif
Przez punkty (x1, f(x1)) i (x2, f(x2)) prowadzimy linię prostą. Jej przecięcie z osią x (y=0) wyznacza punkt (x3,0) którego współrzędna x-owa równa x3 leży bliżej pierwiastka niż x1 i x2. Odrzucamy punkt x1 zastępując go przez x3 i powtarzamy proces sekcji prostą uzyskując nowy punkt (x4, f(x4). W ten sposób dostaniemy ciąg punktów x3, x4, x5, ..., które zbliżają się do pierwiastka równania, a więc do punktu (x*, 0). Ten sposób rozwiązywania problemów nosi nazwę iteracji.
pict/regfal3.gif
Proces poszukiwania pierwiastka powinniśmy kiedyś zakończyć. Można to zrobić np. wtedy gdy |f(x)| < ϵ gdzie ϵ jest bardzo małą liczbą dodatnia. Nie może to jednak być liczba dowolnie mała gdyż nie możemy przekroczyć tutaj możliwości komputera. Z jednej strony nie pozwala na to dyskretna arytmetyka, a z drugiej czas obliczeń. Nie może być on zbyt długi.
pict/regfal4.gif
Może się też zdarzyć, że funkcja, którą dostaliśmy nie posiada miejsc zerowych. Jak to stwierdzić? Co z tym dalej zrobić? Jest jeszcze kilka niejasności, np. jekie ϵ wziąć dla wyznaczenia zbieżności, itd. Zrobimy, pomimo tych trudności, szkic algorytmu. Sformułujmy jeszcze raz lecz teraz już precyzyjniej stojące przed nami zadanie. Program wczyta też dokładność ϵ z jaką ma być wyznaczony pierwiastek x* taki, że |f(x*)| < ϵ, gdzie ϵ > 0. W przypadku znalezienia pierwiastka program ma wypisać informację:
Pierwiastek = xxxxx.xxxx z dokładnością 0.xxxx
A teraz opiszemy słownie co ma zrobić nasz program. Jest to szkic algorytmu. 
START
przeczytaj x1, x2 takie, że leżą one po obu bokach pierwiastka
przeczytaj dokładność epsilon
ustaw wskaźnik znaleziony-pierwiastek na 'nie'
dopóki nie znaleziony-pierwiastek, dopóty wykonuj
   wyznacz x3 metodą sekcji
   jeśli x1 i x
3 są po jednej stronie pierwiastka to
       wstaw do x1 wartość x3
   w innym wypadku
       wstaw do x2 wartość x3
   sprawdź dokładność
   jeśli dokładność < epsilon to
       wstaw do znaleziony-pierwiastek 'tak'
koniec pętli "podczas gdy"
wypisz odpowiedź
STOP
Ogólne sformułowanie, które tu zaprezentowaliśmy jest dość proste. Nie jest jednak precyzyjne. Spróbujmy się zastanowić nad tym co należy udokładnić. 1. Skąd dostaniemy wartości początkowe x1, x2 leżące po bokach pierwiastka? Najprostsza metoda ich otrzymania: od użytkownika programu (nie zawsze dobra). Program sprawdzi tylko czy są one dobre, tzn. czy leżą po przeciwnych stronach; sprawdzanie polega na zbadaniu znaków funkcji f w tych punktach (najlepiej jest zbadać znak iloczynu!). Oto poprawka 
wstaw 'nie' do dobre-dane
dopóki nie (dobre-dane) wykonuj
   jeśli x1 i x2 leżą po obu bokach pierwiastka to 
      wstaw 'tak' do dobre-dane
   w przeciwnym wypadku
      wypisz 'podana wartość x1 i x2 są złe'
         wypisz 'próbuj jeszcze raz'
koniec pętli "d-d"
Chcemy też by program dało się zatrzymać gdy użytkownik nie ma już pomysłów na następną pare danych liczbowych między którymi znajduje się domniemany pierwiastek. Niech więc np. podanie dwu zerowych wartości: 0, 0 zatrzyma program. 
wstaw 'nie' do dobre-dane
wstaw 'nie' do rezygnuje
dopóki nie(dobre-dane), dopóty wykonuj
   wczytaj x1, x2
   jeśli x1 i x2 są zerami to
      wstaw 'tak' do rezygnuje
   w przeciwnym razie
      jeśli x1, x2 leżą po przeciwnych stronach pierwiastka to 
      wstaw 'tak' do dobre-dane
   w przeciwnym wypadku
      wypisz 'podana wartość x1 i x2 są złe'
      wypisz 'próbuj jeszcze raz'
koniec pętli "d-d"
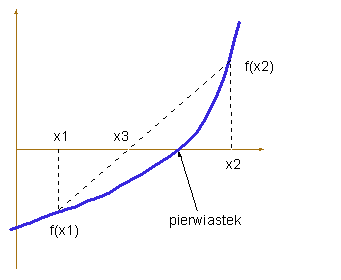
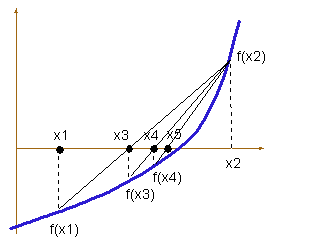
d-d oznacza tutaj w skrócie "dopóki-dopóty". Wartość x3 znajdujemy ze wzoru
x3= x2 f(x1) − x1 f(x2)
f(x1) − f(x2)
Zauważmy, że w przypadku gdy f(x1)=f(x2) to mamy tu dzielenie przez zero! Na szczęście sprawdziliśmy znaki f(x1) i f(x2) i wiemy już w tym miejscu algorytmu, że są one różne, a więc f(x1) i f(x2) są różne i dzielenie przez zero nie ma tu miejsca. Te linie gdzie wyznacza się x3 można teraz zastąpić sekwencją kroków 
wylicz f(x1)
wylicz f(x2)
wstaw (x2 * f(x1) - x1 * f(x2)) / (f(x1) - f(x2)) do x3
Dalej zauważmy, że proces sprawdzania czy punkty x1 i x3 lub x2 i x3 leżą po tej samej stronie pierwiastka polega na sprawdzeniu znaków i odrzuceniu punktu, który ma taki sam znak jak x3. Zapiszemy więc: 
jeśli (f(x1)<0 i f(x3)<0) lub
      (f(x1)>0 i f(x3)>0) to
       wstaw x3 do x1
w przeciwnym razie
       wstaw x3 za x2
Musimy jeszcze zabezpieczyć się przed sytuacją gdy zadana dokładność okaże się za mała, tzn. ϵ będzie tak małe, że program będzie pracować bez skutku, tzn. nie osiągnie tej dokładności, będzie ciągle powtarzał pętlę "dopóki-dopóty". Policzymy w tym celu liczbę przebiegów pętli i zatrzymamy ją gdy liczba ta przekroczy zadaną z góry wartość, która nazwiemy ;licznik. 
wstaw 0 do licznik
dopóki nie (znaleziony-pierwiastek) i (licznik < MaksIter),
  dopóty wykonuj
    ...
    ...
    zwiększ licznik o 1
koniec pętli "d-d"
Zbierzemy teraz wszystkie kawałki algorytmu. Tak, mniej więcej, wygląda cały poprawiony algorytm poszukiwania pierwiastków. Wciąż nie jest on doskonały. Ciągle brakuje mu wielu różnych funkcji (możliwości), ale jak różny jest on od algorytmu wyjściowego! Poprawiliśmy go i ulepszyli w porównaniu z początkowym. 
wstaw 'nie' do dobre-dane
wstaw 'nie' do rezygnuje
dopóki nie(dobre-dane), dopóty wykonuj
   wczytaj x1, x2
   jeśli x1 i x2 są zerami to
      wstaw 'tak' do rezygnuje
   w przeciwnym razie
      jeśli x1, x2 leżą po przeciwnych stronach pierwiastka to 
      wstaw 'tak' do dobre-dane
   w przeciwnym wypadku
      wypisz 'podana wartość x1 i x2 są złe'
      wypisz 'próbuj jeszcze raz'
koniec pętli "d-d"   
wstaw 0 do licznik
dopóki nie (znaleziony-pierwiastek) i (licznik < MaksLIter),
  dopóty wykonuj
   wylicz f(x1)
   wylicz f(x2)
   wstaw (x2 * f(x1) - x1 * f(x2)) / (f(x1) - f(x2)) do x3
   wyznacz x3 metodą sekcji
   jeśli (f(x1)<0 i f(x3)<0) lub (f(x1)>0 i f(x3)>0) to
         wstaw x3 do x1
   w przeciwnym razie
         wstaw x3 do x2
   sprawdź dokładność:
   jeśli dokładność < epsilon to
        wstaw do znaleziony-pierwiastek 'tak'
   zwiększ licznik o 1
koniec pętli "d-d"
wypisz 'Znaleziono pierwiastek x=', wypisz x3
STOP
Uwagi.
Dla skrócenia zapisu można było używac np. konstrukcji a − > b lub b:=a zamiast opisu "wstaw a do b". Podobnie, można używać skrótów P (prawda) lub T (true) zamiast 'tak' oraz F (fałsz lub false). Słowa true i false są slowami zarezerwowanymi w języku Pascal (w Fortran są to .true. i .false.. A teraz kolej na sam program napisany w Pascalu. Tak naprawdę wystarczy przepisać powyższy algorytm prawie dosłownie w języku Pascal (lub Turbo Pascal). 
program regula_falsi;
(*
   Program ma za zadanie znalezc pierwiastki rownania
   f(x)=0 zadanego przez uzytkownika przy zadanej dokladnosci
   obliczen epsilon
*)
function f(x: real): real;
begin
   f:=x*x-10.0
end;
const
   MaksIter = 100;
var
   licznik: integer;      (* licznik iteracji *)
   epsilon: real;         (* wzgledna dokladnosc *)
   rezygnuje: boolean;    (* wskazuje czy opuszczamy dany przedzial *)
   dobre_dane : boolean;  (* wskazuje czy dane x1 i x2 sa OK *)
   znaleziony: boolean;   (* wskazuje czy pierwiastek zostal znaleziony *)
   x1, x2 : real;         (* przedzial zawierajacy pierwiastek *)
   x3 : real;             (* nowy punkt znalezziony metoda regula falsi *)
begin
   (* lokalizujemy przedzial w ktorym jest pierwiastek *)
   dobre_dane:=false;
   rezygnuje:=false;
   while not dobre_dane and not rezygnuje do
   begin
      writeln('Podaj dwa punkty startowe');
      read(x1, x2);
      if (x1=0.0) and (x2=0.0) then
          rezygnuje:=true
      else
          if ((f(x1)<=0.0) and (f(x2)>=0.0)) or
              ((f(x1)>=0.0) and (f(x2)<=0.0)) then
              dobre_dane:=true
          else
          begin
            writeln('Podane liczby nie leza po przeciwnych');
            writeln('stronach pierwiastka. Podaj inne.');
            writeln('Podaj 0, 0 jesli chcesz zatrzymac program')
          end
   end;  petli while 
   if rezygnuje then
      write('Nie znaleziono startowego przedzialu. Stop.')
   else
   begin  rozwiazanie zadania 
      writeln('Podaj dokladnosc rozwiazania');
      read(epsilon);
      znaleziony:=false;
      licznik:=0;
      while not znaleziony and (licznik <= MaksIter) do
      begin
         x3:=(x2*f(x1)-x1*f(x2))/(f(x1)-f(x2));
         if f(x3)=0.0 then (* znaleziono dokladny pierwiastek *)
            znaleziony:=true;
         if ((f(x1)<=0.0) and (f(x3)<=0)) or
              ((f(x1)>=0.0) and (f(x3)>=0.0)) then
              x1:=x3
         else
              x2:=x3;
         licznik:=licznik+1;
         if (abs(f(x3))<=epsilon) then
            znaleziony:=true;
      end; (* petli while *)
      if znaleziony then
         writeln('pierwiastek = ',x3, ' z dokladnoscia ',epsilon)
      else
      begin
          writeln('Po wykonaniu maksymalnej liczby iteracji ', MaksIter);
          writeln('pierwiastka nie udalo sie znalezc')
      end
   end
end.
A oto przykładowe wyniki programu uzupełnionego o dodatkową instrukcje writeln(...): 
writeln(x1:6:3,' ',x2:6:3,' ',x3:6:3,' ',licznik+1:2,
               ' ',abs(f(x3)):8:4,' ',epsilon:10:7);
która pozwoliła na prześledzenie wyników obliczeń w każdym kroku. 
Podaj dwa punkty startowe
1 15
Podaj dokladnosc rozwiazania
.1
WYNIKI:
  x1     x2     x3  licz   f(x3)    epsilon
 1.000 15.000  1.563  1   7.5586  0.1000000
 1.563 15.000  2.019  2   5.9242  0.1000000
 2.019 15.000  2.367  3   4.3975  0.1000000
 2.367 15.000  2.620  4   3.1347  0.1000000
 2.620 15.000  2.798  5   2.1708  0.1000000
 2.798 15.000  2.920  6   1.4734  0.1000000
 2.920 15.000  3.002  7   0.9864  0.1000000
 3.002 15.000  3.057  8   0.6544  0.1000000
 3.057 15.000  3.093  9   0.4315  0.1000000
 3.093 15.000  3.117 10   0.2834  0.1000000
 3.117 15.000  3.133 11   0.1856  0.1000000
 3.133 15.000  3.143 12   0.1214  0.1000000
 3.143 15.000  3.150 13   0.0793  0.1000000
pierwiastek =  3.1497168133E+00 z dokladnoscia  1.0000000000E-01
Program zatrzymał się po wykonaniu 13 iteracji zanim osiągnięta została zadana dokładność 0.1.

Zadanie 1: Metoda bisekcji. Napisać algorytm znajdowania pierwiastka funkcji f(x) zwany metodą bisekcji. Polega on na kolejnym podziale na dwie jednakowe części przedziału (x1, x2), w którym znajduje się pierwiastek i kolejno na przyjęciu, że punkt podziału przybliża pierwiastek równania f(x)=0. Założyć, że dokładność obliczeń ϵ = 1e−6. Narysować schemat N-S algorytmu.

Zadanie 2: Algorytm Newtona. Napisać algorytm rozwiązywania równania f(x)=0 zwany algorytmem Newtona. Algorytm opiera się na rozwinięciu funkcji f(x) w szereg Taylora f(x*)=f(x)+f′(x)(x*−x)+O((x−x*)2), gdzie x* jest domniemanym pierwiastkiem. Na tej podstawie można otrzymać iteracyjny algorytm rozwiązania zadania. Narysować schemat NS algorytmu.

Zadanie 3: Pierwiastki w przedziale. Zmodyfikować wybrany algorytm rozwiązywania równania f(x)=0 tak, by mógł on sam znaleźć wszystkie możliwe rozwiązania w zadanym z góry przedziale lub by wypisał brak rozwiązań jeśli rozwiązania nie istnieją.

File translated from TEX by TTH, version 4.03.
On 16 Oct 2013, 21:50.