Elementy programowania komputerów

Arytmetyka...

Literatura:
O.B. Arushanyan, S.f. Zalotkin, Chyslennye reshenie obyknovennykh differencyalnych uravnenyi.

Podstawy arytmetyki komputerowej

Komputer nie jest idealnym rachmistrzem. Z powodu swojej dyskretnej budowy wciąż robi błędy. Operacje w komputerze wykonywane są na skończonych zbiorach liczb, a nie na wszystkich liczbach rzeczywistych. Podstawowe trzy źródła błędów obliczeń komputerowych:

błędy danych wejściowych
zamiana procesów nieskończonych skończonymi
dokładność reprezentowania liczb w komputerze (zaokrąglenia)

Nie da się uniknąć żadnego z wymienionych błędów. Należy więc kontrolować ich ewolucję w toku prowadzonych rachunków. Zbiór liczb rzeczywistych ma taką własność, że między dowolnie bliskie dwie liczby można wstawić inne. Jest gęsty. Zbiór liczb maszynowych jest natomiast zbiorem dyskretnym, skończonym. Różnice te określają dokładność arytmetyki maszynowej.

Maszynowe systemy liczbowe

Ograniczona długość słów maszynowych, które tworzą elementy pamięci komputerów, pozwala jedynie na to by każda liczba była reprezentowana przez ustaloną liczbę cyfr i znak. Istnieją dwa sposoby reprezentowania liczb w komputerze. § a Część ułamkowa liczby zawiera określoną stałą liczbę cyfr. Jest to reprezentacja z ustaloną kropką dziesiętną, przecinkiem dziesiętnym. Charakteryzują ją trzy parametry:

b - podstawa systemu liczbowego
t - liczba znaków w całej reprezentacji
f - liczba cyfr w części ułamkowej.

Zbiór liczb scharakteryzowany tymi trzema parametrami będziemy dalej oznaczać przez P(b,t,f). Dla przykładu rozpatrzmy zbiór P(10,4,1). Zawiera on 19999 liczb. Kolejne liczby są równoodległe od siebie. Dowolna liczba rzeczywista z przedziału (-1000, 1000) może być zapisana w tym systemie obliczeniowym przez fix(x) ∈ P(10,4,1) z błędem absolutnym nie większym niż 0.05. Np. x=865.54 reprezentowana jest w P(10,4,1) przez 865.5, a błąd absolutny wynosi 0.04. Zobaczmy teraz jak zachowuje się błąd względy (x−fix(x))/x, x ≠ 0. Dla liczby 865.54 błąd względny wynosi 0.04/865.54 ≈ 0.00055 (=0.005%). Z drugiej strony, jeśli x=0.86554 to fix(x)=000.9 i błąd względny wynosi 4%. Oznacza to, że chociaż liczby zbioru P(10,4,1) tworzą sieć jednorodną na przedziale (-1000,1000) to względna gęstość tej sieci nie jest jednorodna. Jest to mankament wszystkich układów z ustaloną kropką. § b Większość komputerów korzysta z innego układu liczbowego F(b,t,L,U) reprezentowania liczb zwanego układem z ruchomą kropką (floating point). Układ taki charakteryzują cztery parametry:

b - podstawa układu liczb
t - liczba cyfr w reprezentacji mantysy liczby (ułamkowej części liczby; dokładność reprezentacji)
L, U - dolna (L) i górna (U) granica przedziału zmienności liczb.

Dowolna, niezerowa liczba jest postaci

x=±(d₁/b+d₂/b²+ ... d_t/b^t)×b^e

i zapisuje się ją jako

x=±d₁d₂... d_t×b^e ,

gdzie cyfry mantysy d₁, d₂, ..., d_t spełniają warunki

1 ≤ d₁ < b , 0 ≤ d_i < b , 2 ≤ i ≤ t ,

a wykładnik e jest liczbą całkowitą taką, że

L ≤ e ≤ U.

Liczba zero jest reprezentowana przez

0=+.000...0×b^L .

Jeżeli dla dowolnego x ∈ F, x ≠ 0, wartość d₁=1 (tak jak to jest w przypadku właśnie wprowadzonego układu F), to taki układ nazywa się znormalizowanym. Liczby należące do F tworzą sieć niejednorodną o jednorodnej gęstości względnej. Dla przykładu rozpatrzmy układ F(10,4,−2,3). Liczbie 865.54 odpowiada w F reprezentant postaci .8655×10³, a liczbie 0.86554 reprezentant .8654×10⁰. W obu wypadkach błędy względne są identyczne i równe 0.005%. Rysunek przedstawia dwa układy zliczania P(2,4,2) i F(2,3,−1,2). P zawiera 31 liczb, a F 33 liczby. 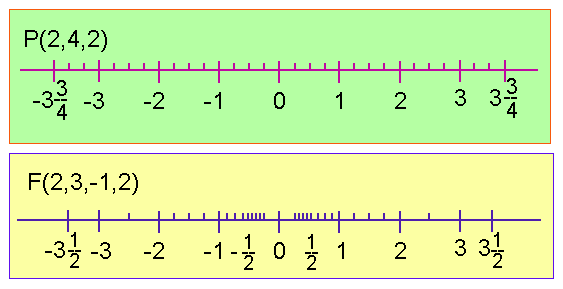pict/ary1rys.png

Ogólnie, układ F zawiera

2(b−1)b^t−1(U−L+1)+1

liczb.

Zadanie 1: Ilość liczb. Ile jest liczb w systemie liczbowym F(10,7,-20,20)?

Parametry arytmetyki maszynowej

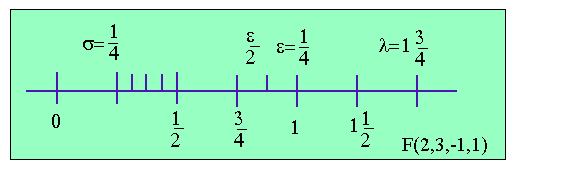
W praktyce, do charakteryzowania układu F(b,t,L,U) używa się parametrów σ, λ, ϵ, które można wyrazić przez b, t, L, U. Zilustrujemy to na przykładzie F(2,3,−1,1). Układ ten zawiera zero oraz wszystkie liczby, których dwójkowa postać jest następująca:

x=±.1d₂d₃×2^e ,

gdzie −1 ≤ e ≤ 1, a d₂ i d₃ są zerem lub jedynką. Mamy dwie możliwości reprezentowania znaku (+ i −), trzy możliwości dla e (−1, 0, 1) oraz cztery możliwości reprezentowania ułamka (0.100, 0.101,0.110, 0.111). Układ F zawiera więc 2·4·3+1=25 liczb maszynowych. W celu uproszczenia rozważań zamienimy ułamki dwójkowe na zwykłe. Mamy w F następujące ułamki: 1/2, 5/8, 3/4 i 7/8. (Np. (0.101)₂=1×2⁻¹+0×2⁻²+1×2⁻³=1/2+1/8=5/8). W rozpatrywanym układzie najmniejszą liczbą jest σ = 1/2×2⁻¹=1/4, a największą λ = 7/8×2¹=7/4 (patrz rysunek). Odległość ϵ między liczbą 1 i liczbą następną układu F ( > 1) nosi nazwę maszynowego epsilon. Jest to jeden z najważniejszych parametrów charakteryzujących dany układ liczbowy. Jest on miarą "dyskretności" układu. pict/ary2rys.png

Ważna własność F: odległość między x ∈ F i liczbą sąsiednią jest nie mniejsza niż |x|ϵ/b i nie większa niż ϵ|x| (jeśli x nie sąsiaduje z zerem). Odległość ϵ/b z lewej strony 1 i epsilon z prawej są ważnymi charakterystykami przy pomiarach odległości między kolejnymi liczbami układu F. Parametry σ, λ i ϵ dane są przez b, t, L i U następująco:

σ = b^L−1 ,

λ = b^U(1−b^−t) ,

ϵ = b^1−t .

W celu lepszego zrozumienia sensu parametrów σ, λ i ϵ rozpatrzmy układ F(b=10, t=6, L=−100). W tym przypadku ϵ = 10⁻⁵, σ = 10⁻¹⁰¹. Prócz tego pomiędzy zerem i σ nie ma żadnej liczby, która należy do F. Jednocześnie w przedziale [σ, 10σ] znajduje się 899999 liczb z układu F. Na ostatnim rysunku widać, że w pobliżu σ odległości między liczbami układu F są mniejsze od σ. Wynika stąd, że liczb tych nie można otrzymać przez dodawanie ich; można je dostać tylko w wyniku obliczania wyrażeń arytmetycznych. Inne własności systemu F. Jeśli L ≤ e < U to pomiędzy liczbami b^e−1 i b^e znajduje się (b−1)b^t−1+1 liczb z F i są one rozłożone jednorodnie z krokiem b^e−t=b^e−1ϵ. Jeżeli x,y ∈ F, b^e−1 ≤ |x| ≤ b^e, b^e−1 ≤ |y| ≤ b^e, to różnica x−y wyliczana jest w F dokładnie, tzn. x−y ∈ F (z pożyczaniem). Odległość między dwoma liczbami z F z wykładnikiem e wynosi b^e−1ϵ. Operacje arytmetyczne nad liczbami z F są przestawne (komutują) jeśli ma miejsce poprawne zaokrąglanie, nie są jednak dla nich spełnione prawa łączności i rozdzielczości. Jeżeli liczbę z F podzielimy (pomnożymy) przez b to odległość od niej do liczby następnej z F zmniejszy się (zwiększy się) dokładnie o czynnik b. Jeżeli x i x+l są sąsiadami z F i liczbę x pomnożymy przez y/ź, gdzie y ∈ F, to pomiędzy y i y+l znajdzie się około |x/y| liczb z F.

Zadanie 2: Granice systemów liczbowych. Podaj najmniejszą dodatnią i największą liczbę w systemie F(10,7,-20,20).

Zadanie 3: Najmniejsza liczba znacząca. Oblicz EPS maszynowe dla systemu liczbowego F(10,7,-20,20).

Błędy zaokrągleń

Zastanowimy się teraz nad różnicami w obliczeniach w układzie liczbowym F i w zbiorze liczb rzeczywistych. Sedno tych róznic polega na tym, że wiele operacji wykonanych na liczbach z F daje wyniki, które do F nie należą. Dlatego też aby pozostać w F (zapisać wynik w pamięci komputera) musimy zastąpić prawdziwy wynik liczbą z F, a więc dokonać przybliżenia. To z kolei oznacza, że pojawił się błąd zaokrąglenia. Mamy tutaj dwa przypadki, w których powstają błędy. Z pierwszym spotykamy się tam gdzie wykładnik e wyniku nie spełnia równości L ≤ e ≤ U. Jeśli e < L, to |x| < σ mamy tzw. antynadmiar, a jeśli e > U to |x| > λ - nadmiar. Drugi przypadek pojawia się tam gdzie mantysa (część ułamkowa) posiada więcej cyfr niż t. Dla przykładu w F(2,3,−1,2) mamy

.110×2⁰+.111×2⁰=.1101×2¹ (3/4+7/8=13/8) .

Wynik dodawania nie należy do F ponieważ do zapamiętania jego mantysy potrzeba czterach cyfr. Podobnie iloczyn

.111×2⁰ ×.110×2⁰=.10101×2⁰ (7/8×3/4=21/32)

nie należy do F. Rozpatrywana sytuacja w przypadku mnożenia pojawia sią bardzo często. Chcąc by wynik leżał w F musimy go więc przybliżyć liczbą z F - zaokrąglić wynik. Można to zrobić na wiele sposobów. Załóżmy, że wynik jest postaci

.d₁d₂... d_td_t+1... d_n ×b^e ,

gdzie L ≤ e ≤ U. Pierwszy sposób zaokrąglania polega na odrzuceniu cyfr d_t+1... d_n po cyfrze d_t Drugi sposób zaokrąglania, zwany prawidłowym polega na wzięciu części ułamkowej zbudowanej z t pierwszych cyfr następującej sumy

d₁ d₂ ... d_td_t+1... + b/2 .

Odpowiada to dodaniu b/2 ×b^−(t+1) do liczby .d₁d₂...d_td_t+1... d_n×b^e. Dla przykładu, liczbie .1101×2¹ w zbiorze F(2,3,−1,2) przypisuje się liczbę .110×2¹ w metodzie odrzucania i liczbę .111×2¹ w metodzie zaokrąglania prawidłowego. Liczbie .10101×2⁰ odpowiada w F .101×2⁰ w obu wypadkach. Podane sposoby zaokrąglania prowadzą do błędów zaokrąglania. Mówiąc dokładniej, błąd zaokrąglania jest różnicą fl(x)−x, gdzie x jest liczbą rzeczywistą z L ≤ e ≤ U, a fl(x) jest jej reprezentacją maszynową. Można wprowadzić wielkość δ(x) zwaną względnym błędem zaokrąglenia, który pojawia się w liczbie fl(x), (x ≠ 0):

δ(x)=(fl(x)−x)/x ,

która spełnia nierówność

|δ(x)| ≤ EPS =

⎧
⎪
⎨
⎪
⎩

b^1−t=ϵ,

odrzucanie

b^1−t/2=ϵ/2,

zaokrąglanie prawidłowe

(*)

Przykład. Pokażemy to. Liczby z przedzialu 〈b^e−1,b^e〉 w systemie z ruchomą kropką są odległe o b^e−t. W przypadku odrzucania (obcinania) młodszych cyfr liczba fl(x) różni się od x nie bardziej niż o b^e−t, a w przypadku zaokrąglania prawidłowego nie bardziej niż o b^e−t/2, tzn.

|fl(x)−x| ≤

⎧
⎪
⎨
⎪
⎩

b^e−t,

obcinanie,

b^e−t/2,

zaokrąglanie prawidłowe .

Ponieważ b^e−1 ≤ x to

|fl(x)−x|/x ≤

⎧
⎪
⎪
⎨
⎪
⎪
⎩

b^e−t

b^e−1

=b^1−t,

obcinanie

b^e−t/2

b^e−1

=b^1−t/2,

zaokrąglanie prawidłowe

Metoda odrzucania jest szybsza od metody zaokrąglania prawidłowego lecz jej dokładność jest dwa razy mniejsza od tej ostatniej. Prócz tego błąd w metodzie odrzucania ma zawsze ten sam znak, przeciwny do znaku zaokrąglanej liczby. Prowadzi to do narastania błedu w przypadku dużych obliczeń. Pomimo tego, że czas wykonania zaokrągleń prawidłowych jest dłuższy w porównaniu z czasem zaokrąglania przez obcinanie, to korzyści z ich stosowania są większe (znoszenie się błędów o przeciwnych znakach).¹ Zilustrujemy teraz zależność (*) w systemie F(10,4,−50,50). Liczbie x=12.467 w F odpowiada przy zaokrąglaniu z odrzucaniem liczba fl(x)=.1246×10²; błąd względny zaokrąglania wynosi

δ(x)=0.007/12.467 ≈ 0.00056 < EPS=10⁻³=0.001 .

Stosując zaokrąglanie prawidłowe mamy natomiast <fl(x)=.1247×10² i

δ(x)=0.003/12.467 ≈ 0.00024 < EPS=10⁻³/2=0.0005 .

Parametr EPS charakteryzuje względną dokładność układu F, a jego wartość zależy od sposobu zaokrąglania. Można go zdefiniować jako najmniejszą liczbę taką, która dodana do 1 w układzie F daje w wyniku liczbę należącą do F i większą od 1:

fl(1+EPS) > 1.

Np. w F(10,4,−50,50) z odrzucaniem, EPS=10⁻³, bo

fl(1+0.001)=fl(.1001×10¹)=.1001×10¹ > 1

i nie można znaleźć liczby mniejszej o tej własności. Jeśli w F stosujemy zaokrąglanie prawidłowe, to EPS=0.0005, bo

fl(1+0.0005)=fl(.10005×10¹)=.1001×10¹ > 1 .

Zadanie 4: Błędy obcinania. Podaj błąd obcinania w systemie F(10,7,-20,20)

Śledzenie błędów zaokrągleń

W fizyce prowadzi się często duże obliczenia numeryczne. Potrzebna jest zawsze wysoka dokładność obliczeń. W jaki sposób błędy zaokrągleń propagują się w czasie obliczeń i jaki jest ich wpływ na końcowe wyniki rachunków? Spróbujemy krótko zastanowić się nad tym problemem. Istnieje wiele sposobów minimalizacji błędów końcowych. Pewne z nich realizuje się sprzętowo (maszyna), a inne programowo (języki). Tutaj będą nas głównie interesować sposóby programowe. 1 Dla przykładu, zastanowimy się jak można uniknąć dużych błędów w przypadku wykonywania operacji prostego wyliczania średniej arytmetycznej (a+b)/2 z liczb a, b. Taka operacja wykonywana jest bardzo często, np. w przypadku wyznaczania pierwiastka równania f(x)=0 na odcinku < a, b > metodą połowienia. Możliwe są dwa sposoby obliczeń!

a+b

(3)

oraz

c=a+

b−a

(4)

Założymy, że obliczenia przeprowadzane są w systemie dziesiętnym z trzema liczbami znaczącymi, z zaokrąglaniem, i a=0.596, b=0.600. Według formuły (3) mamy

c=(0.596+0.600)/2=1.20/2=0.600.

Wartość dokładna jest równa 0.598. Według formuły (4)

c=0.596+(0.600−0.596)/2=1.196/2 ≈ 1.20/2=0.596+0.004/2=0.598.

Zauważymy, że w tym przykładzie, dla którego wzór (4) daje lepszy wynik, obie liczby są jednakowego znaku. 2 Rozpatrzymy przykład obliczeń w systemie dziesiętnym z czterema liczbami znaczącymi, w którym zamiast zaokrąglania stosuje się odrzucanie. Niech a=−3.483, b=8.765. Według (3)

c=(−3.483+8.765)/2=5.282/2=2.641 .

Jest to również wynik dokładny. Według wzoru (4)

c=−3.483+(8.765+3.483)/2=−3.483+12.24/2=−3.483+6.120=2.637 .

Jeśli nawet dokonalibyśmy zaokrąglania to wynik nadal różniłby się od dokładnego gdyż mielibyśmy c=2.642. A więc, w wypadku gdy liczby a i b różnią się znakami, wzór (3) jest lepszy od wzoru (4). Można wyciągnąć wniosek, że najlepsza formuła liczenia średniej polega na tym, by w przypadku gdy (sign(a) ≠ sign(b)) wziąć c=(a+b)/2, a w innym przypadku c=a+(b−a)/2. Teraz już nikt nie powie, że zna dobrze algorytmy numeryczne. Przykład ten pokazuje jakie środki ostrożności należy stosować w przypadku nawet najprostszych operacji i w jaki sposób wybór formuly (algorytmu) może poprawić dokładność programu.

Przykłady dobrych i złych algorytmów

Ostatnie przykłady pokazały, że wielkość błędów zależy od sposobu obliczeń, a więc od przyjętego algorytmu. Podamy jescze inne przykłady algorytmów, które chociaż prawidłowe z formalnego punktu widzenia, mogą spowodować błędy rachunkowe powodowane specyfiką arytmetyki komputera.

Rozwiązywanie równań kwadratowych

Rozpatrzmy równanie

a x²+b x + c=0 .

Pierwiastki tego równania są dane przez formuły

x₁=(−b +

√

b²−4ac

)/2a , x₂=(−b −

√

b²−4ac

)/2a .

Założymy, że rachunki przeprowadzane są w systemie F(10,4, −50,50) z jedną cyfrą zapasową i odrzucaniem młodszych bitów. Niech a=1, b=−320, c=16. Dla wygody, liczby z F będziemy zapisywać w fortranowskiej notacji z E, tzn. ±.d₁d₂d₃d₄Ee, gdzie d_i - cyfra liczby z F, a e - cecha. Np. −320=−.3200×10³ ∈ F w formacie E ma postać −.3200E3. Obliczenia przeprowadzone wg. wzorów dają dla x₁:

x₁

=(.3200E3+

√

.1024E6−.6400E2

/.2000E1

= (.3200E3+.3198E3)/.2000E1

=.6398E3/.2000E1=.3199E3 = 319.9 ,

a dla x₂ mamy

x₂=(.3200E3−.3198E3)/.2000E1=.20000/.2000E1=.1000E0 = 0.1 .

Zostały wyróżnione pierwsze niepewne na skutek zaokrągleń cyfry. Dokładne wartości pierwiastków są równe

x₁=319.950, x₂=0.0500078 .

Stąd, bezpośrednie obliczenia wg. wzorów dla x₁ dały dobry wynik, a dla x₂ zły gdyż względny błąd obliczeń x₂ wynosi 100%. Łatwo zrozumieć dlaczego tak się stało. W liczniku ułamka dla x₂ obliczana jest różnica dwóch dużych liczb 320 i 319.8. Z tego powodu ich starsze cyfry wzajemnie się znoszą, a wynik odejmowania określają ich młodsze cyfry. Ponieważ ostatnia cyfra liczby 319.8 zawiera błędy zaokrąglania, więc wynik operacji odejmowania jest bezwartościowy ponieważ jego pierwsza cyfra znacząca jest obarczona błędem. Taka sytuacja nosi nazwę katastrofalnej utraty dokładności. Powstaje ona zawsze tam gdzie odejmowane są bliskie sobie liczby. Prowadzi to do wzrostu poziomu błędów obliczeń. Można uciec od katastrofy utraty dokładności stosując inny algorytm obliczeń. W rozpatrywanym przypadku należy zastosować następujące wzory rachunkowe

x₁ = (−b−sign(b)

√

b²−4 a c

)/(2 a) , x₂=c/(a x₁) ,

gdzie sign(b) oznacza znak liczby b. Dla wybranych poprzednio wartości a, b, c mamy

x₂=

.1600E2

.3199

=.5002E−1=0.05002 .

Rozsądny wybór algorytmu ustrzegł nas przed niepotrzebnymi błędami. Należy o tym pamiętać.

Obliczanie funkcji eksponencjalnej

Załóżmy, że chcemy zbudować algorytm obliczania funkcji eksponencjalnej e^x słuszny dla dowolnych x. Ponieważ w rachunkach funkcja ta będzie pojawiać się bardzo często chcemy by jej wartość była maksymalnie dokładna. Założymy, że w tym celu postanowiliśmy wykorzystać rozkład e^x w szereg

e^x=1+x+

x²

x³

+ ... ,

który jest zbieżny dla dowolnych rzeczywistych i zespolonych x. W obliczeniach numerycznych musimy ograniczyć ilość składowych szeregu do skończonej ich liczby. Liczba ta zależy od x i od żądanej dokładności. Załóżmy że należy wyliczyć wartość e^−5.5 w systemie arytmetycznym F(10,5,−50,50). Mamy e^−5.5= 1.0000
-5.5000
+15.125
-27.730
+38.129
-41.942
+38.446
-30.208
+20.768
-12.692
+6.9803
- 3.4902
+ 1.5997
...
-----
+0.0026363.
Szereg został ucięty do 25 składowych ponieważ dalsze składowe nie mają już wpływy na wartość jego sumy w arytmetyce F. Otrzymaliśmy więc maksymalnie dokładny wynik w F. Wynik dokładny jest jadnakże równy 0.0408677! Znów mamy do czynienia z katastrofalną utratą dokładności. Wynika to z analizy wartości składowych szeregu. Młodsza cyfra znacząca każdej składowej większej co do modułu od 10 wpływa na starszą cyfrę wyniku. Ponieważ składowe szeregu są wyliczone w przybliżeniu to fakt ten wyjaśnia błąd wyniku końcowego. Aby uniknąć powstałej sytuacji wystarczy obliczyć dyskutowaną metodą e^5.5, a następnie odwrócić otrzymany wynik:

e^−5.5=

e^5.5

=1/(1+5.5+15.125+...)=0.0040865 .

Pokazany przykład posiada czysto ilustracyjny charakter. Zbieżność zastosowanego szeregu jest bardzo słaba, a to prowadzi do dużej liczby składowych o ile chcemy zapewnić żądaną dokładność obliczeń. W praktyce do obliczeń e^x stosowane są bardziej efektywne algorytmy. Rozpatrzone przykłady pokazują w jakim stopniu metoda numeryczna może zależeć od małych zmian parametrów, a więc danych początkowych. Przykładowo, niech w problemie równania kwadratowego parametr b=−320.0 zostanie zamieniony na −320.1. Dla x₂ obliczanego według wzoru wyjściowego otrzymamy 0.05. Stąd, zmiana o 0.03% tylko jednego współczynnika prowadzi do zmiany wyniku o 200%. (Zauważmy, że dokładna zmiana pierwiastka spowodowana zamianą b jest równa 0.03%. Dokładny pierwiastek jest równy 0.0499922.) Stosowany wzór jest wrażliwy na parametry z przedziału b < 0 i b² >> 4ac; w innych przypadkach pracuje on całkiem dobrze. Problem numeryczny może więc w pewnych przypadkach zależeć silnie od wartości początkowych, a w innych nie. Ponieważ błędy zaokrągleń można traktować jako niewielkie zmiany danych początkowych więc stosowanie algorytmu, który jest wrażliwy na tego typu zmiany może okazać się niebezpieczne. Należy w takich przypadkach poszukiwać metod alternatywnych.

Obliczanie pierwiastków wielomianów

Poprzednie przykłady pokazują, że metoda numeryczna (algorytm) może silnie reagować na małe zmiany danych początkowych. Pokażemy teraz, że istnieją problemy, które same w sobie są czułe na tego typu zaburzenia. Klasycznym przykładem są obliczenia pierwiastków wielomianu

p(x)=(x−1)(x−2)...(x−20)=x²⁰−210x¹⁹+...

Wielomian ten posiada dobrze odseparowane pierwiastki 1, 2, 3, ..., 20. Załóżmy, że współczynnik przy x¹⁹ został zaburzony i jest równy −(210+2⁻²³). Nowy wielomian nieznacznie różni się od wyjściowego wielomianu p(x) lecz jego pierwiastki różnią się bardzo. Zapiszemy ich wartości z dokładnością do pięciu cyfr po przecinku:

1.00000 ,

10.09527±0.64350 i ,

2.00000 ,

11.79363±1.65232 i ,

3.00000 ,

13.99236±2.51883 i ,

4.00000 ,

16.73074±2.81262 i ,

5.00000 ,

19.50244±1.94033 i ,

6.00001 ,

20.84691 .

6.99970 ,

8.00727 ,

8.91725 ,

Widać wyraźnie, że niewielkie zaburzenie wielomianu p(x) doprowadziło do znacznych zmian pierwiastków, a niektóre z nich stały się nawet zespolone Nie miało to miejsca w przypadku dyskutowanego wcześniej równania kwadratowego. Tam, wystarczyła zmiana algorytmu. Tutaj, w przypadku wielomianu p(x) problem jest sam z siebie czuły na zmiany parametrów. Niezależnie od metody obliczeń, wprowadzenie błędów zaokrąglania, a więc zaburzenie, zawsze doprowadzą do znacznych zmian w pierwiastkach.

Układ równań liniowych

Przykładem problemu, który jest mało stabilny jest układ równań

11x+10y+4z

=1,

12x+11y−13z

=1,

14x+13y−66z

=1.

Dokładnym rozwiązaniem jest x=1, y=−1, z=0. Załóżmy, że zaburzymy prawą stronę układu zastępując (1, 1, 1) przez (1.001,0.999, 1.001). Rozwiązanie wzięte z trzema cyframi znaczącymi jest w tym przypadku dane przez: x=−0.683, y=0.843, z=0.006. Widzimy, że zaburzenie prawej strony o 0.1% doprowadziło do wyniku różnego od poprzedniego o 175% licząc w stosunku do maksymalnie zmienionego pierwiastka.

Inne przykłady

Rozpatrzmy jeszcze parę przykładów, które demonstrują w jaki sposób propagują się błędy zaokrągleń.

Przykład algorytmu niestabilnego

Załóżmy, że chcemy obliczyć całkę

E_n=

⌠
⌡

1

0

xⁿ e^x−1 dx, n=1, 2, ... .

Zachodzi następujący związek rekurencyjny

E_n=xⁿ e^x−1 |₀¹ −

⌠
⌡

1

0

xⁿ⁻¹e^x−1=1−nE_n−1, n=2, 3, ... E₁=1/e.

Jeśli wykonamy obliczenia według pokazanego schematu w układzie F(10,6,−50,50) otrzymamy

E₁

≈

0.367879 , E₆ ≈ 0.127120 ,

E₂

≈

0.264242 , E₇ ≈ 0.110160 ,

E₃

≈

0.207274 , E₈ ≈ 0.118720 ,

E₄

≈

0.170904 , E₉ ≈ −0.0684800 .

E₅

≈

0.145480 ,

Jedyny błąd zaokrąglania pojawił się w przybliżeniu E₁ ≈ 1/e i doprowadził do tego, że E₉ jest ujemna chociaż wiadomo, że w przedziale (0,1) funkcja x⁹e^x−1 jest dodatnio określona i E₉ ≈ 0.0916123. Inne błędy w procesie rekurencyjnych obliczeń E₉ nie zostały wprowadzone. Przyczyną tak szybkiego wzrostu błędu jest fakt, że początkowy błąd równy 4.412×10⁻⁷ przy obliczaniu E_n jest mnożony przez n!. W szczególności, przy n=9 błąd w E₉ jest równy 4.412×10⁻⁷×9! ≈ 0.1601 i jest prawie równy rzeczywistej wartości E₉. W ten sposób wybrany algorytm okazał się niestabilnym ponieważ w każdym kroku błędy stają się coraz większe. Jeśli zapiszemy nasz algorytm w postaci

E_n−1=

1−E_n

, n = ..., 3, 2 ,

to łatwo zauważyć, że w n-tym kroku błąd nie powiąksza się, lecz zmniejsza się n razy, tzn. dany algorytm jest stabilny. Widomym jego mankamentem jest to, że nie znamy początkowego przybliżenia. Niezależnie jednak od tego z jakim błędem wybierzemy początkową wartość dla n >> 1 błędy będą bardzo szybko maleć w każdym kroku obliczeń. Możliwe do przyjęcia przybliżenie początkowe może być oszacowane następująco

E_n=

⌠
⌡

1

0

xⁿ e^x−1 dx ≤

⌠
⌡

1

0

xⁿ dx =

xⁿ⁺¹

n+1

|₀¹ =

n+1

Jeśli weźmiemy np. E₂₀ ≈ [1/21] to błąd przy E₁₉ będzie już pomnożony przez 1/20 i będzie wynosił 0.0024. Kiedy dojdziemy do E₁₅ błąd będzie mniejszy od 4×10⁻⁸ (a więc mniejszy od rzeczywistego błędu zaokrąglenia) i będzie malał z powodu stabilności metody. Poczynając od E₁₅ wartości E_n są dokładne do szóstego miejsca co odpowiada możliwości zaokrągleń na ostatnim miejscu.

Czy zawsze 10×0.1=1?

Rozpatrywany przykład jest cenny z tego względu, że liczba 0.1 często brana jest jako wielkość kroku przy całkowaniu równań różniczkowych oraz jako parametr w innych algorytmach numerycznych. Jeśli maszyna korzysta z układu dziesiętnego, tzn. b=10 wówczas równość 10×0.1=1 jest bezwarunkowo spełniona. Jeżeli b=2 to tak nie jest ponieważ 0.1 nie posiada skończonego rozwinięcia w potęgi 2⁻¹. Rzeczywiście, w układzie dwójkowym 0.1 jest równe

(0.1)₁₀=(0.0001100110011...)₂ .

W niektórych komputerach reprezentacja 0.1 ma w Fortranie postać

(0.1)₁₀=2⁻³×0.

1100110011... 001100

40−miejsc

| 11 ... .

Widać stąd, że kompilator wziął 0.1 z niedomiarem gdyż miejsce 41-e zawiera 1. Jeśli pomnożymy tę wielkość przez 10 (na komputerze) i odejmiemy od wyniku jedynkę to otrzymamy 2⁻⁴⁰ ≠ 0. Jeśli przedstawimy 0.1 jako 1/10 to po wykonaniu dzielenia w komputerze otrzymamy inną reprezentację liczby 0.1:

(0.1)₁₀=2⁻³×0.

110011001100...001101

W tym przypadku 10×0.1=1. Zobaczmy teraz, czy spełniona jest równość

10
∑
1

0.1 = 0.1+0.1+... +0.1 = 1 .

Ponieważ rozwinięcie dwójkowe 0.1 jest nieskończone to odpowiedź jest negatywna. W przypadku rozpatrywanej reprezentacji różnica między 1 i sumą ∑₁¹⁰ 0.1 wynosi 2⁻³⁹−2⁴⁰.

Propagacja błędów danych początkowych w algorytmach rozwiązań zwyczajnych równań różniczkowych

Rozważmy prosty przykład numerycznego rozwiązywania problemu Cauchy'ego zwykłego równania różniczkowego

y′=λy , y(0)=y₀ .

(1)

Rozwiązaniem jest funkcja

y(x)=y₀e^λx .

Przeanalizujemy algorytm Eulera z ustalonym krokiem h. Przybliżone rozwiązanie (1) u_n+1 w punkcie x_n+1 jest dane przez²

u_n+1

u_n+hf(x_n,u_n)

(2)

(1+hλ)u_n

(3)

(1+hλ)² u_n−1

(4)

...

(5)

(1+hλ)ⁿ⁺¹u₀ .

(6)

Wielkość u₀ jest przybliżeniem wartości początkowej y₀. Różnica między u₀ i y₀ może pochodzić z niedokładności w danych początkowych lub z błędów zaokrągleń maszynowych. Mogą też wystąpić obie te przyczyny jednocześnie. Wielkość u₀ zawiera więc błąd e₀=y₀−u₀. Zauważmy także, że w metodzie Eulera używamy przyliżenia 1+hλ funkcji e^λx. Zapiszemy teraz wyrażenie określające globalny błąd E_n+1 w (n+1)-szym kroku całkowania. Ponieważ

u_n+1=(1+hλ)ⁿ⁺¹u₀=(1+hλ)ⁿ⁺¹(y₀−e₀) ,

to błąd E_n+1 jest równy

E_n+1

y_n+1−u_n+1

(7)

y₀e^(n+1)hλ−(1+hλ)ⁿ⁺¹(y₀−e₀)

(8)

[e^(n+1)hλ−(1+hλ)ⁿ⁺¹]y₀ +(1+hλ)ⁿ⁺¹e₀ .

(9)

Globalny błąd posiada dwie składowe. Pierwsza pochodzi z przybliżenia funkcji e^hλ przez (1+hλ), druga opisuje propagację błędu e₀ z warunku początkowego. Jeśli |1+hλ| > 1, to składowa druga rośnie ze wzrostem n i w ostateczności staje się dominującą częścią globalnego błędu E_n+1. Jeżeli chcemy ograniczyć propagację błędu dla przypadku λ < 0 musimy zadbać o to by spełniony był warunek

|1+hλ| < 1 lub h < 2 / |λ| .

Otrzymany warunek na ograniczenie kroku całkowania h nosi nazwę warunku stabilności. W przypadku jego niespełnienia przybliżone rozwiązanie problemu będzie niestabilne. Tak więc maksymalna wartość kroku całkowania h_max zależy zarówno od parametrów problemu (w naszym przypadku od parametru λ) jak również od zastosowanego algorytmu obliczeń. Warunek stabilności h < 2/|λ| został otrzymany z konkretnej aproksymacji 1+hλ funkcji e^hλ. W jednym z algorytmów rozwiązywania równań różniczkowych, tzw. metodzie Runge-Kutta 4-go rzędu, funkcję e^hλ aproksymuje się wyrażeniem

e^hλ=1+hλ+

(hλ)²

(hλ)³

(hλ)⁴

To nakłada inne ograniczenia na h. W tym przypadku dokładne wyznaczenie warunku stabilności w jawnej postaci jest trudne do wyliczenia, można jednak powiedzieć, że stabilność ma miejsce dla takich h, dla których wartości przedstawionego wielomianu są absolutnie mniejsze od 1. Jeżeli λ > 1 to nierówność 1+hλ > 1 jest spełniona dla dowolnego h > 0, a to oznacza, że w każdym kroku procesu całkowania obserwuje się wzrost błędów lokalnych. W tym wypadku niestabilność nie jest oczywista ponieważ dominującą składową błędu globalnego E_n+1 staje się w tym wypadku pierwsza składowa. Niezależnie od tego jak mały krok h wybierzemy, różnica e^(n+1)hλ−(1+hλ)ⁿ⁺¹ będzie przy dostatecznie dużych n większa od (1+hλ)ⁿ⁺¹. Tego typu problem nosi nazwę źle uwarunkowanego. Jeśli w analogiczny sposób przeprowadzimy analizę ogólnego przypadku y′=f(x,y), to można dojść do następujących ogólnych wniosków:

W wielu problemach znak ∂f/∂y zmienia się w przedziale całkowania, tzn. błędy lokalne są raz mniejsze, a raz większe. W tym wypadku dobrze jest wykonać całkowanie tak by wiedzieć jaki jest znak ∂f/∂y i w ten sposób kontrolować sytuację. W prostym przypadku y′=λy, λ > 0 lepiej jest całkować w kierunku mniejszych x, tzn, z ujemnym krokiem h. Oczywiście, każde równanie różniczkowe wymaga oddzielnego podejścia.

Zadanie 5: Liczby dwójkowe. Zapisz w systemie binarnym liczby 2013, 777, 100, 0.1

Zadanie 6: Różne systemy liczbowe. Zapisz liczby z zadania poprzedniego w systemie ósemkowym i szesnastkowym

Zadanie 7: Systemy. Napisać (Fortran) program przeliczania liczb z jednego systemu liczbowego (inpsys) do innego (outsys)

Zadanie 8: Systemy liczbowe. Napisz program w Pascalu, który wszystkie działania (+,-,*,/) będzie wykonywał w arytmetyce F(b,t,L,U), gdzie danymi będą b, t, L i U.

Footnotes:

¹Załóżmy, że wszystkie błędy zaokrągleń są tej samej wielkości, ich znaki są niezależne i pojawiają się jednakowo często. Z centralnego twierdzenia granicznego teorii prawdopodobieństwa wynika, że prawdopodobny błąd sumy n dodatnich składników przy stosowaniu metody odrzucania jest w przybliżeniu √n razy większy niż błąd metody zaokrąglania prawidłowego. ²Ogólnie y′=f(x,y) i rozwiązania poszukujemy zapisując pochodną y′ w postaci y′=(y_n+1−y_n)/h, gdzie y_n=y(x_n), i x_n+1=x_n+h, co wynika z definicji pochodnej, a więc jest słuszne dla h→ 0.

File translated from T_EX by T_THgold, version 4.00.
On 30 Oct 2013, 10:58.