Dynamiczne struktury danych
Zmienna dynamiczna jest to zmienna, która pojawia się (i znika) wtedy gdy jest potrzebna (lub nie jest) podczas wykonywania się programu. Zwykłe zmienne statyczne , istnieją przez cały czas wykonywania się programu. Odwołania do zmiennych dynamicznych odbywają się poprzez wskazy1, a nie przez nazwy definiowane przez użytkownika, jak to ma miejsce w przypadku zwykłych zmiennych statycznych.Wskazy.
Sytuację tę możemy graficznie przedstawić tak jak pokazano niżej.
|
-->( type )-->[ Nazwa typu ]-->( = )-->( ^ )-->[ Typ bazowy ]-->( ; )-->Przykład.
type intwskaz=\^{~}integer;\\
var iw: intwskaz;
W ten sposób iw jest zmienną wskazującą wielkości
typu integer. Wartość zmiennej wskazanej przez iw
jest zadana przez iw^.
|
Przykład. Innym przykładem jest zmienna wk typu wrek zdefiniowana następująco:
type wrek=^kalendarz
kalendarz=record
miesiac: (Sty,Lut,Mar,Kwi,Maj,Cze,Lip,Sie,Wrz,Paz,Lis,Gru);
dzien : 1..31
end;
var
wk: wrek;
Zmienna wk jest wskazem do zmiennej o dwóch polach skalarnych:
miesiac i dzien.
|
wk^.miesiac wk^.dzienIstnieją dwie procedury Turbo Pascala, które tworzą lub usuwają (niszczą) zmienne dynamiczne. Są to new(p)
oraz
dispose(p) Wywołanie procedury new(p) powoduje nadanie wartości wskazowi p oraz utworzenie zmiennej wskazywanej przez p. Wywołanie podprogramu dispose(p) powoduje zwolnienie pamięci zarezerwowanej dla zmiennej wskazywanej przez p oraz "wyzerowanie" p: p=nil. Wielkość nil jest słowem zarezerwowanym języka Pascal i oznacza "nic". Zmienna o wartości nil nic nie pokazuje. Wskazy mogą pokazywać złożone struktury danych Pascala. Mogą to być np. drzewa binarne (patrz dalej).
A
/\
/ \
/ \
/ \
B E
/\ /\
/ \ / \
/ \ / \
C D F G
/ /\
I J K
/ \
Drzewo binarne
type
wskaz=^wezel;
wezel=record
lewywskaz : wskaz;
nazwa : char
prawywskaz: wskaz;
end;
var p, root: wskaz;
Każdy węzeł zawiera trzy pola: dwa wskazania do innych
węzłów, lewego i prawego (lewywskaz, prawywskaz) oraz
"wartość", nazwa, którą jest pojedynczy znak.
Chcę zwrócić uwagę, że nie deklarujemy zmiennych typu
wezel lecz wskazy! do zmiennych tego typu. Są to wskazy
p oraz root.
Chcąc utworzyć drzewo o jednym węźle napiszemy
new(root); { rezerwacja miejsca + nadanie wartości
zmiennej root }
root^.nazwa:='a'; { definicja pola nazwy węzła }
root^.lewywskaz:=nil; { brak węzła z lewej strony }
root^.prawywskaz:=nil; { brak węzła z prawej strony }
Schematycznie ygląda to następująco:
|
|
new(p); { rezerwacja miejsca + nadanie wartości
zmiennej p }
root^.prawywskaz:=p; { prawy wskaz pokazuje nowy węzeł }
p^.nazwa:='b'; { definicja pola nazwy węzła }
p^.lewywskaz:=nil; { brak węzła z lewej strony }
p^.prawywskaz:=; { brak węzła z prawej strony }
Jeśli teraz chcielibyśmy usunąć utworzony właśnie węzeł, zapiszemy:
root^.prawywskaz:=nil;
dispose(p) { usuwa zarezerwowaną wcześniej przestrzeń
zajmowaną przez zmienną wskazywaną przez p }
Listy jednostronne. Przykładem zastosowania rekordów
i wskazów jest jednostronna lista połączona. Jest to struktura, której węzły zawierają dane i pokazują następne elementy listy.
|
|
Przykład.
type
wsk=^spotkania;
spotkania=record
dane=record
osoba: array[1..20] of char;
godzina: 0..23;
minuta: 0..59
end;
nastepny: wsk { wskaz do następnego spotkania }
end;
var
naglowek: wsk;
Zadanie 1: Organizator spotkań. Napisz program, organizator spotkań, który pozwala założyć i modyfikować listę spotkań (wstawiać, usuwać). Elementami listy niech będą godzina, minuta, osoba (nazwisko) i miejsca spotkania (adres).
Macierze kwadratowe.
Duże macierze kwadratowe, np. macierz o wymiarach 5000×5000, czyli zawierająca 25000000 elementów, stwarzają duży problem numeryczny. Jak zorganizować dane i program, który musi nimi operować? Jednym z możliwych rozwiązań jest następujące. Można wczytywać z pliku jeden wiersz macierzy i mieć szybki dostęp do 5000 elementów na raz. Co jednak zrobić gdy potrzebne są dwa lub więcej wierszy na raz? Tak jest np. w przypadku mnożenia macierzy.Zadanie 2: Złożoność. Napisz program, który czyta plik z tablicą liczb rzeczywistych o wymiarach 1000 ×1000. Oceń stopień złożoności programu. Znajdż czas obliczania sumy elementów takiej tablicy.
Zadanie 3: Wyznacznik. Policz wyznacznik tablicy 1000 ×1000 złożonej z liczb losowych z przedziału <0,1> wygenerowanych przez funkcje rand() Turbo Pascala.
Literatura: Cormen Leiserson, Rievest, ...
Do dynamicznych struktur danych należą stosy, kolejki, drzewa itp. Jak zawsze, z każdym typem danych, związane są typowe dla danej struktury operacje. Operacje wykonywane na zbiorach dynamicznych, takie jak wstawianie elementów, usuwanie elementów oraz sprawdzanie przynależności elementu do zbioru można podzielić na zapytania i operacje modyfikujace. Są to Search, Insert, Delete, Minimum, Maximum, Successor, Predecessor, itp. W kolejnych częściach omówimy różne struktury danych dynamicznych wraz z odpowiadającymi im operacjami.Stosy, kolejki, listy, drzewa
Stos S jest dynamiczną strukturą danych, w której
element najpóźniej dodany do struktury usuwany jest jako pierwszy (Last in, First out; jest to tzw. struktura LiFo). Zwyczajowo, operacja Insert nosi nazwę Push, a operacja Delete nazywa się Pop. Przykłady: stos talerzy w barach samoobsługowych, stos rozkazów i danych w pamięci komputera, itp. Stos o liczbie elementów nie większej niż n można zaimplementować w tablicy S[1..n]. Dodatkowa cecha (atrybut) top[S] określa aktualną długość stosu S. Elementem na dnie stosu jest S[1], a S[top[S]] jest ostatnim elementem stosu. Jeśli top[S]=0 to stos jest pusty (Stack-Empty). Próba zdjęcia elementu ze stosu pustego nazywa się niedomiarem., W przypadku gdy top[S] > n (przekroczona dopuszczalna długość stosu) mówimy, że stos jest przepełniony. Poniżej przedstawione są algorytmy typowych operacji na stosach.Stack-Empty(S) 1 if top[S]=0 2 then return True 3 else return False Push(S,x) 1 top[S] <- top[S]+1 2 S[top[S]] <- x Pop(S) 1 if Stack-Empty(S) 2 then error ,,niedomiar'' 3 else top[S] <- top[S]-1 4 return S[top[S]+1]Rysunek przedstawia działanie operacji Push i Pop na stosie S.

Zadanie 4: Palindromy. Napisać program, który rozpoznaje palindromy, wykorzystując stos i operacje na stosie.
Kolejki reprezentują np. kolejki ludzi na poczcie, w banku lub
sklepie, kolejka samochodów na skrzyżowaniu, itp. Operacja wstawiania do kolejki nazywana jest Enqueue, a operacją usuwania elementu z kolejki jest Dequeue. Kolejka posiada początek, head (głowę) oraz koniec tail (ogon). Element może być usunięty z kolejki jeśli tylko wtedy gdy znajduje się na jej początku. Rysunek poniżej przedstawia implementację kolejki o maksymalnej liczbie elementów n−1=10 oraz działanie operacji Enqueue i Dequeue na tej kolejce. Tutaj przyjęto, że tablica reprezentująca kolejkę jest cykliczna, tzn. pozycja o numerze 1 jest następnikiem pozycji o numerze n.
Enqueue(Q,x) /* wstaw element x do kolejki */ 1 Q[tail[Q]] <- x 2 if tail[Q]=length[Q] 3 then tail[Q] <- 1 4 else tail[Q] <- tail[Q]+1 Dequeue(Q) /* Usun element z kolejki */ 1 x <- Q[head[Q]] 2 if head[Q]=length[Q] 3 then head[Q] <- 1 4 else head[Q] <- head[Q]+1 5 return
Zadanie 5: Kolejki. Kolejka dwustronna (dwukierunkowa) jest strukturą danych pozwalającą na wstawianie i usuwanie elementów na obu jej końcach. Napisz cztery procedury, służące do wstawiania i usuwania elementów z obu końców kolejki przechowywanej w tablicy.
Zadanie 6: Kolejki i stosy. Pokaż, jak zaimplementować kolejkę, używając dwóch stosów. Oszacuj czas działania operacji na takiej kolejce.
Zadanie 7: Stosy i kolejki. Pokaż, jak zaimplementować stos za pomocą dwóch kolejek. Oszacuj czas działania operacji na takim stosie.
Lista z dowiązaniami jest strukturą danych, w której elementy
są ułożone w liniowym porządku. Porządek wyznaczają indeksy, wskazy, związane z każdym elementem listy. Lista posiada początek (head) i koniec (tail). Elementy listy mają swoje poprzedniki (prev, od previous) oraz następniki (next). Często mamy doczynienia z listami posortowanymi. Operacje związane z listami to: wyszukiwanie, wstawianie elementów i usuwanie elementów. Elementy listy składają sie z pól zawierających wskazy do elementów poprzedniego i następnego. Jeśli takich elementów nie ma to wskaz zawiera wartość Nil. Oprócz pól zawierających wskazy, elementy listy zawierają pola zwane kluczami (key). Pola te mogą być dowolnego typu. Mogą to być np. różnego rodzaju rekordy itp. Przykład bardzo prostej listy pokazany jest na rysunku.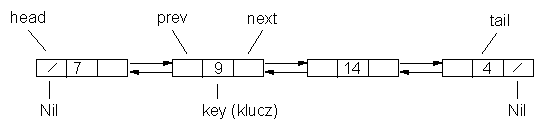
List-Search(L,k) 1 x <- head[L] 2 while x <> Nil i key[x] <> k 3 do x <- next[x] 4 return List-Insert /* wstaw na poczatek listy L */ 1 next[x] <- head[L] 2 if head[L] <> Nil 3 then prev[head[L]] <- x 4 head[L] <- x 5 prev[x] <- NilAlgorytm ten pozwala wstawiać element x na początek listy. Następny algorytm usuwa element listy. W realizacji list za pomocą tablic wartość usuwanego elementu tablicy pozostaje niezmieniona. W ten sposób zaśmieca się pamięć (tablicę) reprezentującą listę. Podobnie dzieje się gdy korzystamy bezpośrednio z zasobów pamięci komputera używając wskazów.
List-Delete(L,k) 1 if prev[x] <> Nil 2 then next[prev[x]] <- next[x] 3 else head[L] <- next[x] 4 if next[x] <> Nil 5 then prev[next[x]] <- prev[x]Jeśli udałoby się pominąć warunki brzegowe dotyczące głowy i ogona listy dwukierunkowej, wówczas treść procedury Delete byłaby prostsza.
List-Delete(L, x) 1 next[prev[x]] <- next[x] 2 prev[next[x]] <- prev[x]Można to osiągnąć wprowadzając tzw. wartownika, który jest elementem NIL listy. Jeśli każdy wskażnik do Nil zamienimy wskaźnikiem do wartownika to lista staje się listą cykliczną.
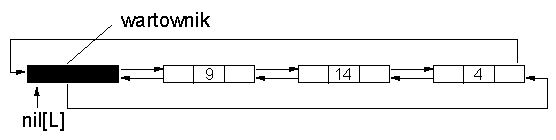
Zadanie 8: Listy. Napisać procedurę List-Search i List-Insert dla przypadku listy cyklicznej (z wartownikiem).
Zadanie 9: Sortowanie list. Napisać procedurę, która łączy dwie listy jednokierunkowe, posortowane w jedną listę posortowaną i jednokierunkową, bez używania wartowników. Następnie, zmodyfikować ją dodając wartownika o kluczu ∞ na koniec każdej z list. Porównać stopień komplikacji obu procedur.
Zadanie 10: Odwracanie list. Napisać nierekurencyjną procedurę odwracającą kolejność elementów listy jednokierunkowej, działającą w czasie Θ(n). Dodatkowa pamięć (oprócz tej zajętej przez listę) powinna być stała (tj. niezależna od liczby elementów na liście).
Drzewa binarne są w zasadzie połączonymi listami, w których
każdy węzeł (ojciec) może zawierać wskazy do pary synów: lewego i prawego. Najwyższy węzeł nosi nazwę pnia (korzenia). Drzewa zawierające tylko węzeł główny noszą nazwą drzew o zerowej wysokości (czasami o jednostkowej). Każdy nowy poziom węzłów (znajdujących się na jednakowej wysokości) zwiększa wysokość drzewa o jeden. Drzewo całkowicie wypełnione posiada 2wysokość drzewa węzłów. Drzewo poszukiwań binarnych (binary search tree, BST) jest drzewem o uporzadkowanych węzłach, przy czym, porządek węzłów zadany jest wg. jakiejś operacji binarnej lub boolowskiej. Najczęściej porządek jest następujący. Numer schodzącego węzła porównywany jest z numerem pnia i jeśli jest on mniejszy lub równy numerowi pnia to węzeł umieszczany jest z lewej jego strony. W przeciwnym wypadku węzeł umieszczany jest po prawej stronie pnia. Operacja powtarzana jest na każdym poziomie drzewa, aż do momentu gdy osiągnie się poziom ostatni gdzie umieszcza się ów węzeł. W ten sposób drzewo posiada strukturę logiczną. Istnieje kilka metod przechodzenia (przemiatania) drzewa binarnego. Są to metoda preorder, metoda inorder oraz metoda postorder. Metoda preorder polega na wypisaniu klucza pnia drzewa w pierwszej kolejności, a następnie jego lewego poddrzewa. W następnym kroku przechodzi się do poddrzewa prawego. W każdym przypadku (lewego lub prawego poddrzewa) stosuje się również metodę preorder. W metodzie postorder wypisuje się klucz korzenia po wypisaniu wartości znajdujących się w poddrzewach: lewym i prawym. W metodzie przechodzenia drzewa zwanej inorder klucz korzenia wypisuje się pomiędzy kluczami z jego poddrzewa lewego i poddrzewa prawego.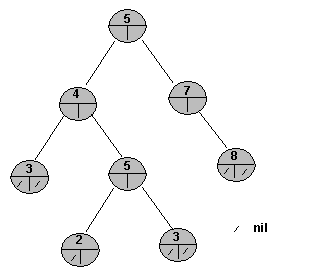
Zadanie 11: Skanowanie drzewa. Zaprojektuj algorytmy przechodzenia drzewa metodami inorder, postorder i preorder.
Zadanie 12: Drzewa. Narysuj drzewa poszukiwań binarnych o wierzchołkach (węzłach) 1, 4, 5, 10, 16, 17, 21 o wysokościach 2, 3, 4, 5.
Pliki są strukturami danych które zawierają sekwencje elementów
jednego typu. Dostęp do nich, w przeciwieństwie do tablic, jest sekwencyjny, tzn. element pliku jest dostępny gdy odpowiedni wskaz pokazuje ten element (patrz niżej).Przykład. Zadeklarujemy kilka typów plikowych.
type
PlikDanych: file of integer;
PlikKolorow: file of (r, g, b);
PlikZnakowy: file of char;
Plik Tablic: file of array [1..10] of real;
PlikPersonaliow: file of
record
Nazwisko: array [1..20] of char;
RodzajZatrudnienia: (stałe, godzinowe, zlecone)
end; { rekordu }
var
x: PlikDanych;
y: PlikKolorow;
z: PlikTablic;
Spis: PlikPersonaliow;
Podanie po zmiennej plikowej znaku ^ pozwala wyłuskać
wartość zmiennej z pliku (lub wstawić ją).
Np. xôznacza liczbę całkowitą, y^jest jedną z wartości
r, b lub g koloru. z^jest tablicą 10-o elementową.
Pisząc z^[7] mamy dostęp do 7-go elementu tej tablicy.
Pola rekordów z pliku Spis osiągalne są za pomocą konstrukcji:
Spis^.Nazwisko[1] ... Spis^.Nazwisko[20] Spis^.RodzajZatrudnieniaFunkcje związane z plikami (file) Z typami danych deklarowanych z pomocą file of wiążą się funkcje operujące na tych strukturach. Są to
- eof(plik) - boolean, = true jeśli jest koniec struktury plik;
- reset(plik) - ustawia wskaz do pierwszego elementu struktury plik; pozwala czytać plik;
- rewrite(plik) - ustawia plik do zapisu; eof(plik)=true;
- get(plik) - przesuwa wskaz do następnego elementu pliku i pobiera ten element; ...
- put(plik) - dopisuje do pliku odpowiadający element
- eoln(plik) - boolean; =true jeśli koniec linii
- read(plik, znak) - czytanie znaku;
- readln(plik, znak) -
z:=plik^; while not eoln(plik) do get(plik); get(plik); - write(plik, z) - plik^:=z; put(plik);
- writeln(plik,z) -
z:=plik^; put(plik); plik^:="znl"; put(plik);Tutaj znl jest znakiem nowej linii.
Footnotes:
1Czasami używa się też nazwy wskaźniki co może się mylić ze wskaźnikami tablic lub nazwy angielskiej pointers.File translated from TEX by TTH, version 4.03.
On 16 Oct 2013, 21:50.

