Temat: Zależne od czasu równanie Schrödingera. Ruch pakietów falowych. Schemat jawny, stabilny i unitarny.


Na podstawie: H.M. Schey. J.L. Schwartz, Computer-Generated Motion Pictures of One-Dimensional Quantum Mechanical Transmission and Reflection Phenomena, Am. J. Phys. , 35 (1967) 177

1 Unitarność

Pokazany w poprzednim wykładzie schemat iteracyjny rozwiązania równania Schrödingera zależnego od czasu jest schematem jawnym (tzn. ψn+1 jest wyliczane na podstawie poprzedniego kroku ψn) lecz nie jest schematem unitarnym. Operator ewolucji exp(±i∆t ∧H) zastąpiliśmy tam wyrażeniem 1±i∆t∧H, które nie zapewnia unitarności funkcji falowej (∫|ψ|2dx ≠ 1). Podobnie jest z prostymi schematami niejawnymi opartymi na tym wyrażeniu. Eliminują one niestabilność numeryczną lecz problem niezachowania unitarności wciąż pozostaje. Przyjrzyjmy się stabilnej metodzie niejawnej. Otrzymamy ją następująco. Funkcja falową ψn+1 w chwili ∆t potraktujmy chwilowo jako daną. Na jej podstawie wyliczmy ψn. Ponieważ ψ(∆t) = exp(−i∆t H)ψ(0)}, więc ψ(0) = exp(i∆t ∧H)ψ(∆t). Stąd, rozwijając w szereg Taylora, mamy
ψjn = ψjn+1−(i∆t/∆x2) [ ψj+1n+1 − 2ψjn+1−ψj−1n+1 − ∆x2 Vj ψjn+1] .
Równanie to, chociaż stabilne, daje niejawnie ψn+1. Metoda jest, jak to nazywamy, typu implicit. Aby wyznaczyć ψn+1 potrzeba stosować specjalne techniki algebraiczne. Ważniejszy jest jednak problem unitarności ψ.

1.1 Postac Cayley'a operatora ewolucji

Prostym przybliżeniem operatora ewolucji exp(i∆t ∧H) jest jego postać Cayleya
(1− 1
2
 ∆t
^
H
 ) / (1− 1
2
 ∆t
^
H
 ) ,
(1)
która dodatkowo zapewnia dokładność do rzędu ∆t2. Stosując postać Cayleya operatora ewolucji możemy teraz zapisać
ψjn+1 = (1− 1
2
 ∆t
^
H
 ) / (1− 1
2
 ∆t
^
H
 )ψjn ,
(2)
Po prostych obliczeniach dostaniemy następujacy schemat różnicowy
ψj+1n+1 + (i 2 ∆x2
∆t
 − ∆t2 Vj − 2)ψjn+1 + ψj−1n+1 =
− ψj+1n + (i 2 ∆x2
∆t
 + ∆t2 Vj + 2)ψjn − ψj−1n .
(3)
Równanie to jest stabilne, zapewnia unitarność, lecz nie daje jawnie wartości dla ψn+1.

2 Metody stabilne, unitarne i jawne

Na podstawie: Richardson, John L., Visualizing quantum scattering on the CM-2 supercomputer, Computer Physics Communications 63 (1991) pp 84-94

Dyskutowane poprzednio metody były oparte na przybliżeniu dla operatora ewolucji funkcji falowej, który jest formalnym rozwiązaniem równania Schrödingera. Równanie ewolucji jest postaci
ψ(x, t) = exp(−i t−t0
ħ
^
H
 ) ψ(x, t0) .
(4)
Najprostsza metoda (niestabilna) była oparta na przybliżeniu
exp(−i ∆t
ħ
^
H
 ) = 1 − i ∆t
ħ
^
H
 + O([ ∆t
ħ
^
H
 ]2) .
(5)
Prowadziło to do rozbieżności metody. Drugie przybliżenie było oparte na postaci Cayleya operatora ewolucji (patrz 1). Ta metoda była wprawdzie stabilna numerycznie lecz niejawna i kosztowna numerycznie gdyż wymagała złożonych obliczeń prowadzących do rozwikłania niejawnego schematu ewolucji. Metoda, którą podaje Richardson, jest również oparta na przybliżeniu operatora ewolucji, lecz jest to metoda zarówno jawna, jak i unitarna, i stabilna numerycznie. Operator ewolucji zapisywany jest najpierw w postaci sumy operatora energii kinetycznej ∧T i potencjalnej ∧V. Dalej ∧T rozbija się na sumę M częsci ∧T = ∑l=1M∧Tl, dla których łatwo jest policzyć exp∧Tl. Następnie korzystamy z tzw. przybliżenia iloczynowego Trottera:
exp(−i ∆t
ħ
^
H
 ) = ⎛
⎝ 		M
∏
j=1
exp(−i ∆t
ħ
^
H
 )⎞
⎠ 		exp(−i ∆t
ħ
^
V
 ) + O(∆t2)
(6)
Błąd jaki tutaj popełniamy zależy od wartości komutatorów [Tl,Tl′], [Tl, V] i od wielkości kroku czasowego ∆t. W przypadku jednego wymiaru przestrzennego podział operatora ∧T można określić z formuły różnicowej dla Laplasjanu:
(
^
T
 ψ)n = ħ2
2ma2
 [2ψn − ψn−1 − ψn+1] .
Macierz T jest postaci
[T] = ħ2
2ma2
 ⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
2
−1
0
...
0
−1
−1
2
−1
...
0
0
−1
2
−1
...
0
...
0
...
−1
2
−1
−1
0
...
0
−1
2
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
(7)
Macierz ta daje się zapisać jako suma następujących macierzy
[Te] = ħ2
2ma2
 ⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
M
0
0
...
0
0
M
0
...
0
...
0
...
0
M
0
0
0
...
0
M
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
(8)
oraz
[To] = ħ2
2ma2
 ⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
1
0
0
...
−1
0
M
0
...
0
0
0
M
...
0
...
0
...
0
M
0
−1
0
...
0
1
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		,
(9)
gdzie M jest macierzą kwadratową 2×2
M = ħ2
2 m a2
 ⎛
⎜
⎜
⎝
1
−1
−1
1
⎞
⎟
⎟
⎠ 		.
(10)
Macierze [Te] i [To] są sumami prostymi macierzy M. Łatwo jest obliczyć exponentę macierzy M. Mamy mianowicie
exp(−i ∆t
ħ
M)
=
1+[exp(−iϵ)−1] m a2
ħ2
=
1
2
 ⎛
⎜
⎜
⎝
1 + exp(−iϵ)
1−exp(−iϵ)
1 − exp(−iϵ)
1+exp(−iϵ)
⎞
⎟
⎟
⎠ 		= 1
2
 ⎛
⎜
⎜
⎝
α
β
β
α
⎞
⎟
⎟
⎠
(11)
gdzie ϵ = ∆tħ/ma2, a α = 1 + exp(−iϵ)/2 i β = 1 − exp(−iϵ)/2. Macierz exp(−i[(∆t)/(ħ )] M) jest unitarna i posiada wartości własne λ1=1, λ2=exp(−iϵ).
Z a d a n i e 1. Proszę sprawdzić słuszność ostatniej formuły. Obliczyć wartości własne M i exp(−iϵM).
Zapiszmy wyniki w postaci operatorowej
(
^
T
e
ψ)n = ħ2
2ma2
 ⎛
⎝ 		ψn − 1
2
 (1 − (−1)n) ψn−1− 1
2
 (1 + (−1)n)ψn+1⎞
⎠ 		,
(12)

(
^
T
o
ψ)n = ħ2
2ma2
 ⎛
⎝ 		ψn − 1
2
 (1 + (−1)n) ψn−1− 1
2
 (1 − (−1)n)ψn+1⎞
⎠ 		.
(13)
Exponenta tych wyrażeń jest postaci
⎧
⎨
⎩ 		exp(−i∆t/ħ
^
T
e
ψ)⎫
⎬
⎭
n
= ⎛
⎝ 		αψn − β
2
 (1 − (−1)n) ψn−1− β
2
 (1 + (−1)n)ψn+1⎞
⎠ 		,
(14)

⎧
⎨
⎩ 		exp(−i∆t/ħ
^
T
o
ψ)⎫
⎬
⎭
n
= ⎛
⎝ 		αψn − β
2
 (1 + (−1)n) ψn−1− β
2
 (1 − (−1)n)ψn+1⎞
⎠ 		.
(15)

2.1 Równanie dyfuzji

Wyniki dotyczące stabilności, dyskutowane tutaj dla przypadku równania Schrödingera, są również słuszne dla równania dyfuzji. Podstawienie t→−it i V=0 przekształca wszystkie wzory otrzymane dla równania Schrödingera w klasyczne równanie dyfuzji. Operatory unitarne zamieniane sa rzeczywistymi operatorami o wartościach własnych mniejszych niż jeden i stabilność metody jest zapewniona.

2.2 Więcej wymiarów

W przypadku większej liczby wymiarów wyrażenia są niewiele bardziej skomplikowane.
Z a d a n i e 2. Otrzymać wzory różnicowe dyskutowanej metody dla przypadku n-wymiarowego równania Schrödingera lub równania dyfuzji.

3 Problemy graficzne

Ponieważ dyskutowane wyżej problemy można przedstawić graficznie zajmiemy się przez chwilę sposobami reprezentacji danych na ekranie. Dyskusja będzie dotyczyć trzech spraw. Pierwsza to proste rzutowanie figur 3 wymiarowych, druga to rysowanie poziomic (konturów), a trzecia to problem niewidocznych linii na rysowanych rzutach.

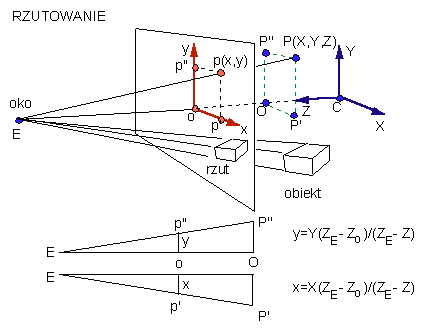
3.1 Rzutowanie

pic//proj.gif
Rzutowanie figur na ekran. (Patrz tekst)
Łatwo sprawdzić słuszność następujących równości
x
=
|OP′| ·|EO| / |EQ| = X(ZE − ZO)/(ZE − Z)
(16)
y
=
Y(ZE − ZO) / (ZE − Z)
(17)
Z a d a n i e 3. Napisz program w JavaTM (klasa), który rzutuje figurę o zadanych wierzchołkach (xi,yi,zi) na ekran. Zastosuj do kilku wybranych figur przestrzennych.

3.2 Poziomice

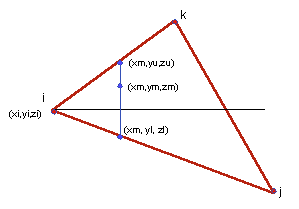
Poziomice są liniami jednakowej wartości funkcji z=f(x,y), a więc określone są równaniem z=const. Najwygodniej jest podzielić obszar określoności funkcji f na trójkątne podobszary. Interpolacja wielkości z w takim elementarnym obszarze trójkąta przebiega następująco (patrz rysunek).
pic//interp.gif
Interpolacja $z$ w punkcie wewnętrznym $(x_m,y_m)$ trójkąta (i-j-k).
Najpierw znajdujemy najdalej wysunięte punkty w x:
xmin = min(xi, xj, xk) , xmax = max(xi, xj, xk) .
W celu zbadania całego obszaru trójkąta przesuwamy linię x = xm od xmin do xmax. Dla każdej wartości xm znajdujemy granice zmienności y. Nazwiemy je yl oraz yu. Są one ograniczone dwoma bokami trójkąta i−j−k. Trzeci bok nie jest ważny i wykluczymy go z rozważań. Aby sprawdzić, który to bok sprawdzamy czy xm leży poza przedziałem (xp, xq), gdzie p, q = i, j, k. Jeśli np. xm leży poza przedziałem (xk, xj) (patrz rysunek), to bok ij wykluczamy z procedury znajdowania yu i yl dla x = xm. Jeśli xm przekroczy xk to znajdzie się na zewnątrz (xi, xk) i w konsekwencji wykluczymy bok ik. Jeśli będziemy wyznaczać xu i xl z równań boków ik oraz ij, jak na rysunku, to dostaniemy
yu = yi + (yk − yi) (xm − xi) / (xk − xi) ,

yl = yi + (yj − yi) (xm − xi) / (xj − xi) .
Jeżeli xk = xi lub xj = xi to yu i yl są równe maksymalnej i minimalnej wartości y. Podobne formuły interpolacyjne stosujemy dla z otrzymując zu i zl w punktach (xm, yu) i (xm, yl) (wystarczy zamienic y-ki przez z-ty w równanich). Znajomość granic zl i zu na linii xm pozwala znaleźć wartość z w punkcie ym przez interpolację
z(xm, ym) = zm = zl + (ym − yl) (zu − zl) / (yu − yl) .
Zmieniając xm w granicach (xmin, xmax i ym oraz ym w granicach (yl, yu) możemy znaleźć z we wszystkich interesujących nas punktach trójkąta i−j−k. Należy przy tym dobrać wielkość przyrostów ∆x, ∆y tak by otrzymać w miarę gładkie krzywe.
Z a d a n i e 4. (Dla zainteresowanych) Napisz program dokonujący triangulacji dziedziny z=f(x,y) i znajdujący poziomice z=const.

3.3 Problem niewidocznych linii

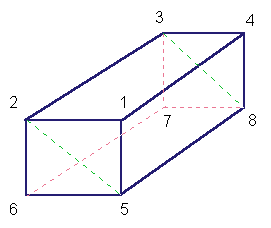
Które linie rysowanej na ekranie figury są widoczne, a które nie? Jak je odróżnić? Problem ten prosto opisał H.N. Lerman (Software Age, July, 1970). Aby zrozumieć na czym to polega spójrzmy na rysunek prostopadłościanu.
pic//cegla.gif
Prostopadłościan.
Zewnętrzne wierzchołki prostopadłościanu wraz z łżczącymi je krawędziami są zawsze widoczne. Wewnętrzne wierzchołki mogą być albo widoczne albo niewidoczne. Zależy to od tego, "z której strony kartki papieru" znajduję one się znajduje, a więc zależy to od wartości współrzędnej z wierzchołka. Np., jeśli kartka papieru (ekran) ustawimy tak by przechodził przez z=0 to wierzchołki o z < 0 (i punkty linii o z < 0 ) nie powinny pojawić się na rysunku.
Z a d a n i e 5. (Dla zainteresowanych) Napisz program który rysuje powierzchnię z=f(x, y) bez linii niewidzialnych.