Temat: Modele przeciekania (percolation)
Algorytmy stosowane w tzw.
modelach perkolacyjnych (przeciekania). Przejście fazowe. Próbkowanie
Monte Carlo. Zadania.
Na podstawie: Binder, Heermann, Monte Carlo simulations in statistical
physics, Springer, 1997
1 Model przeciekania
Rozpatrujemy problem obsadzania węzłów nieskończonej sieci.
Prawdobieństwo obsadzenia węzła jest równe p. Prawdopodobieństwo,
że węzeł pozostaje pusty wynosi 1−p. Sąsiadujące obsadzone węzły
tworzą tzw. klastry. Istnieje krytyczne pc takie, że dla p < pc
na sieci istnieją tylko klastry o skończonych rozmiarach l,
natomiast przy p > pc istnieje jeden klaster, który przecieka
z jednego brzegu sieci do przeciwnego.
Algorytm przeciekania jest bardzo prosty. Dla sieci 3-wymiarowej
o rozmiarze L można go zapisać następująco.
for (i=0;i<L;i++)
for(j=0;j<L;j++)
for(k=0;k<L;k++)
lattice[i][j][k] = Math.random()<p?1:0;
Jeden przebieg przez wszystkie węzły sieci wyznacza całą konfigurację.
Problemy:
- Ile klastrów nl(p), zawierających l węzłów istnieje na sieci
w przeliczeniu na jeden węzeł?
- Czy istnieje klaster rozciągający się od brzegu do brzegu?
- Ile wynosi pc?
- Jakie jest prawdopodobieństwo, że obsadzony węzeł neleży do
klastra przeciekającego, tzw. prawdopodobieństwo przeciekania, P∞(p)?
- Czemu równa się podatność χ zdefiniowana wzorem:
(Prim oznacza, że w sumowaniu pominięto największy klaster).
Typowy algorytm obliczeń polega w tym problemie na wygenerowaniu N
konfiguracji i na uśrednieniu odpowiednich wielkości.
1 powtarzaj konfig = 1 aż do N
2 utwórz konfigurację
3 przeanalizuj konfigurację
4 wylicz interesujące wielkości
5 dodaj odpowiadające wyniki
6 wykonaj uśrednianie
Analiza konfiguracji (3) polega na przeliczeniu klastrów i wyznaczeniu
ich rozmiarów. Jak zidentyfikować klastry? Klaster jest takim zbiorem
węzłów, że każdy element zbioru posiada sąsiada należącego do tego zbioru.
Obsadzone węzły można traktować jak graf. Graf może składać się
z oddzielnych podgrafów. Istnieją grafy z jednym wierzchołkiem, dwoma,
trzema itd. Zadanie polega na przeliczeniu podgrafów w każdej klasie.
Jak sprawdzić, że klaster jest nieskończony? Zadanie sprowadza się do
sprawdzenia czy istnieje ścieżka łącząca dwa przeciwległe brzegi sieci.
Prawdopodobieństwo znalezienia takiej ścieżki określa tzw. parametr
porządku Ps, który może być następnie użyty do wyznaczenia punktu
przejścia pc. Poniżej pc prawdopodobieństwo znalezienia takiej
ścieżki jest zerowe, gdyż istnieją tylko klastry skończone. Powyżej
progu pc istnieje klaster nieskończony, który pozwala na przejście
od brzegu do brzegu sieci; parametr porządku skacze gwałtownie do
jedynki.
Z a d a n i e 1.
Znaleźć algorytm rozstrzygający czy w danej konfiguracji problemu
przeciekania istnieje ścieżka, łącząca przeciwne brzegi sieci.
Wyznaczyć parametr porządku Ps dla różnych sieci o wielkości L
i dla różnych prawdopodobieństw p. (Za parametr porządku w danej
konfiguracji przyjąć stosunek wielkości największego klastra do
liczby wszystkich obsadzonych węzłów sieci.)
2 Modelowanie wielkości losowych
Na podstawie: Sobol
Nie bądziemy omawiać sposobów generowania liczb losowych
z jednorodnym rozkładem prawdopodobieństwa na odcinku (0, 1),
zakładając, że są one znane.
Zajmiemy się, krótko, metodami otrzymywania wartości wielkości
losowych występujacych z zadanymi, acz niejednorodnymi, rozkładami
prawdopodobieństwa.
Przedyskutujemy najczęściej stosowaną metodę, tzw. funkcji
odwrotnych.
2.1 Metoda funkcji odwrotnych
Funkcją rozkładu dowolnej wielkości losowej nazywamy funkcję
Jej dziedziną jest −∞ < x < ∞. Można pokazać, że F(x)
jest monotonicznie rosnąca i, że 0 ≤ F(x) ≤ 1. Dalej
limx→−∞F(x)=0, limx→∞F(x)=1. (F nie jest
ściśle monotoniczna i może być nieciągła.)
Przy założeniu ścisłej monotoniczności i ciągłości y = F(x) istnieje
funkcja odwrotna x = G(y) taka, że dla wszystkich
−∞ < x < ∞ i przy 0 < y < 1 mamy
|
G(F(x)) = x, F(G(y)) = y . |
|
Pokażemy, że wielkość losowa G(x) posiada rozkład F(x)
Mamy
|
P{ G(γ) < x } = P{ F(G(γ)) < F(x) } = P{ γ < F(x) } . |
|
Ponieważ γ posiada rozkład jednorodny na (0, 1) to
prawdopodobieństwo P{ γ < F(x) } = P{ 0 < γ < F(x) }
jest równe długości odcinka (0, F(x)), czyli równa się F(x).
Pokazaliśmy więc, że
Co nam to daje? Jeśli ξ posiada rozkład F(x), gdzie F(x) jest
ściśle monotoniczna i ciągła, to wielkość ξ można modelować wg.
wzoru
Ponieważ γ posiada taki sam rozkład na (0, 1) jak
1 − γ, to można tez używać równoważnej formuły
Sposób wyznaczania wielkości losowych ξ wg. tych formuł
nosi nazwę metody funkcji odwrotnych.
2.1.1 Normalna wielkość losowa
Normalna wielkość losowa ξ ∈ (−∞, ∞) ma rozkład
prawdopodobieństwa
|
p(x) = |
1
|
exp |
(x−a)2
2σ2
|
, |
|
gdzie a, σ > 0 i
2.1.2 Całka prawdopodobieństwa
|
Φ(x) = |
2
|
| ⌠
⌡
|
x
0
|
exp−t2/2 dt . |
|
Podstawienie t1=(x′−a)/σ, t2=(x"=a)/σ daje
|
P{ x′ < ζ < x" } = |
1
2
|
[Φ(t2) − Φ(t1)] . |
|
Biorąc x′=a−3σ, x"=a+3σ otrzymamy
|
P{ a−3σ < ζ < a+3σ} = Φ(3) ≈ 0.997 . |
|
(Prawo 3-ech sigm) Widzimy, że otrzymujemy prawie jednostkowe
prawdopodobieństwo otrzymania zdarzenia z przedziału
a−3σ < ζ < a+3σ.
3 Zastosowania metody MC
Na podstawie: Rozdzial jest tłumaczeniem rozdziału 9 książki Sobola
Temat: Zastosowanai MC
Całki oznaczone
Na podstawie: Sobol, Metoda Monte Carlo, wyd. ros., Nauka, 1985.
Moje nieudolne tłumaczenie z rosyjskiego; tylko dla studentów.
4 §9. Obliczanie całek oznaczonych
Problemy, które rozpatrywaliśmy w poprzednich rozdziałach, były
statystycznymi z natury i wykorzystanie metody Monte Carlo przy ich
rozwiązywaniu było w ich przypadku rzeczą naturalną.
Tutaj rozpatrujemy problem matematyczny przybliżonego obliczenia
całki oznaczonej.
Ponieważ obliczanie takich całek jest równoznaczne z wyznaczaniem
pól, to można byłoby wykorzystać metodę p. 1.2. Zamiast tego
opiszemy inną, bardziej efektywną metodę, która pozwala budować
różne modele stochastyczne rozwiązywania tego problemu metodą Monte
Carlo. Pokażemy też jak wybrać spośró nich model najlepszy.
9.1. Metoda obliczeń.
Rozpatrzmy funkcją g(x), określoną na przedziale a < x < b. Chcemy
w przybliżeniu obliczyć całkę
(jeśli jest to całka niewłaściwa to żądamy, że jest ona absolutnie
zbieżna).
Weźmy dowolną gęstość p(x) na (a, b) (tzn. dowolną funkcję
p(x), spełniającę warunki (15), (16)). Wraz z losową wielkością
ξ, określoną na przedziale (a, b) z gęstością p(x),
potrzebna będzie wielkość
Zgodnie z (18)
|
Mη | ⌠
⌡
|
b
a
|
|
g(x)
p(x)
|
p(x) dx=I . |
|
Rozpatrzmy teraz N jednakowych, niezależnych wielkości losowych
η1, η2, ..., ηN i zastosujmy do sumy tych
wielkości centralne twierdzenie graniczne. Formuła (21) jest w tym
wypadku
|
P | ⎧
⎨
⎩
| ⎢
⎢
|
1
N
|
|
N
∑
j=1
|
ηj−I | ⎢
⎢
|
< 3 |
⎛
√
|
| ⎫
⎬
⎭
|
≈ 0.997 . |
|
Ostatnia równość mówi, że jeżeli weźmiemy N wartości
ξ1, ξ2, ..., ξN to przy odpowiednio dużym N
|
|
1
N
|
|
N
∑
j=1
|
|
g(ξj)
p(ξj)
|
≈ I . |
|
Jednocześnie, z bardzo dużym prawdopodobieństwem błąd
przybliżenia (34) nie przewyższa 3√{Dη/Ń}.
9.2. Istotny wybór.
Widzieliśmy, że w celu obliczenia całki (33) można wykorzystać
dowolną wielkość losową ξ, określoną na przedziale (a, b)
z gęstością p(x) > 0.1 W dowolnym przypadku Mη = M[g(ξ)//p(ξ)]=I.
Jednakże dyspersja Dη, a wraz z nią oszacowanie błędu
w formule (34) zależą od tego jaka wielkość ξ jest
wykorzystywana, gdyż
|
Dη = Mη2−I2= | ⌠
⌡
|
b
a
|
|
g2(x)
p(x)
|
dx−I2 . |
| (35) |
Pokażemy, że wielkość ta jest minimalna, gdy p(x) jest
proporcjonalne do |g(x)|.
Wykorzystamy w tym celu znaną z analizy matematycznej nierówność
|
| ⎛
⎝
| ⌠
⌡
|
b
a
|
|u(x)v(x)| dx | ⎞
⎠
|
2
|
≤ | ⌠
⌡
|
b
a
|
u2(x) dx | ⌠
⌡
|
b
a
|
v2(x) dx , |
|
w której wstawimy u=g(x)//√{p(x)}, v=√{p(x)}. Otrzymamy
|
| ⎛
⎝
| ⌠
⌡
|
b
a
|
|g(x)| dx | ⎞
⎠
|
2
|
≤ | ⌠
⌡
|
b
a
|
|
g2(x)
p(x)
|
dx | ⌠
⌡
|
b
a
|
p(x) dx= | ⌠
⌡
|
b
a
|
|
g2(x)
p(x)
|
dx . |
| (36) |
Z (35), (36) wynika, że
|
Dη ≤ | ⎛
⎝
| ⌠
⌡
|
b
a
|
|g(x)| dx | ⎞
⎠
|
2
|
−I2 . |
| (37) |
Pozostaje pokazać, że dolną granicę wartości dyspersji (37)
otrzymamy biorąc gęstość p0(x)=c|g(x)|. Łatwo to zrobić, gdyż
z warunku unormowania p0(x) wynika, że
|
c= | ⎛
⎝
| ⌠
⌡
|
b
a
|
|g(x)| dx | ⎞
⎠
|
−1
|
. |
|
Oznacza to, że
|
| ⌠
⌡
|
b
a
|
|
g2(x)
p0(x)
|
dx= |
1
c
|
| ⌠
⌡
|
b
a
|
|g(x)| dx = | ⎛
⎝
| ⌠
⌡
|
b
a
|
|g(x)| dx | ⎞
⎠
|
2
|
, |
|
i prawa strona (35) przechodzi w prawą stronę (37).
Nie da się praktycznie wykorzystać najlepszej gęstości p0(x),
gdyż potrzebna jest w tym celu znajomość całki
∫ab|g(x)| dx. Wyliczenie jej jest z kolei problemem,
równoważnym wyznaczeniu całki (33). Z tego względu zaleca się
by g ę s t o ś ć p(x) b y ł a p r o p o r c j o n a l n a
d o |g(x)|.
Wybór bardzo złożonych p(x) jest oczywiście niecelowy ponieważ
procedura wyboru ξ stanie się zbyt pracochłonna. Można
jednak kierować się tym przy wyborze p(x) (patrz p. 9.3).
Oszacowanie (34) z gęstością p(x) zbieżną z |g(x)|, nazywamy
istotnym wyborem.
W praktyce, całek postaci (33) nie wylicza się metodą Monte Carlo;
istnieją bardziej dokładne metody obliczeń - wzory kwadraturowe.
Przy przejściu do całek wielokrotnych sytuacja ulega zmianie: wzory
na kwadratury stają się zbyt zawiłe, a metoda Monte Carlo prawie
się nie zmienia.
5 Neutrony
Na podstawie: Rozdzial jest tłumaczeniem rozdziału 7§8 książki Sobola
Temat: Zastosowania MC
Przechodzenie neutronów przez materię; rozbłyski gamma
Na podstawie: Sobol, Metoda Monte Carlo, wyd. ros., Nauka, 1985.
Moje nieudolne tłumaczenie z rosyjskiego. Tylko dla studentów.
6 §7. Przechodzenie neutronów przez płytkę
Znane są prawa statystyczne oddziaływania pojedynczych cząstek
elementarnych (neutronu, fotonu, mezonu, i innych) z materią.
Zazwyczaj istnieje potrzeba znalezienia makroskopowych charakterystyk
procesów, w których bierze udział ogromna liczba takich cząstek:
gęstości, prądów, itp. Sytuacja jest podobna do rozpatrywanej w §§5,
6 i nadaje się do wykorzystania w niej metody Monte Carlo.
Bodaj najczęściej metoda Monte Carlo stosowana jest w fizyce
neutronów. Rozpatrzymy prostszy wariant problemu przechodzenia
neutronów przez płytkę.
7.1. Sformułowanie problemu.
Niech na nieskończoną, jednorodną płytkę o grubości 0 ≤ x < ≤ h
pada strumień neutronów o energii E0. Kąt padania wynosi
90o. Podczas zderzeń z atomami materiału, z którego zbudowana jest
płytka, neutrony mogą rozpraszać się elastycznie lub mogą być
pochłaniane. Założymy, że energia neutronu nie ulega zmianie przy
w procesie rozpraszania i dowolny kierunek odbicia neutronu od
atomu jest jednakowo prawdopodobny (ostatnia własność jest czasami
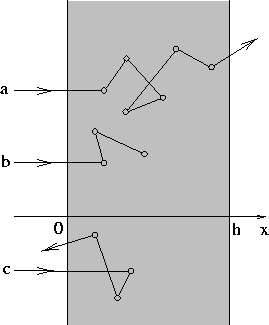
widoczna w materiałach zbudowanych z ciężkich atomów). Na rys. 22
pokazano różne warianty oddziaływania neutronów z płytką: a-neutron
przechodzi przez płytkę, b-neutron jest pochłaniany w płytce,
c-neutron jest odbity przez płytkę. Należy wyliczyć
prawdopodobieństwo przejścia neutronu przez płytkę p+,
prawdopodobieństwo odbicia neutronu p− i prawdopodobieństwo
pochłaniania neutronu przez płytkę, p0.
Oddziaływanie neutronów z materiałem charakteryzujemy w rozważanym
przypadku dwoma parametrami stałymi, Σc i Σs, które
nazywają się przekrojem czynnym na pochłanianie (ang.
capture (c) - wychwyt) oraz przekrojem czynnym na
rozpraszanie (ang. scattering (s) - rozpraszanie).
Suma obu przekrojów nosi nazwę całkowitego przekroju czynnego
Przekrój czynny ma następujący sens fizyczny. Prawdopodobieństwo
wychwytu neutronu jest równe Σc//Σ, a prawdopodobieństwo
rozpraszania jest Σs//Σ.
Droga swobodna neutronu λ (tzn. długość drogi od zderzenia
do zderzenia) jest wielkością losową. Może przyjmować dowolne
wartości dodatnie z gęstością prawdopodobieństwa
Łatwo zauważyć, że podana gęstość wielkości λ pokrywa
się z gęstością (26) wielkości losowej τ, najprostszego
strumienia zgłoszeń. Analogicznie do p. 5.2 można od razu napisać
wyrażenie dla średniej drogi swobodnej:
oraz podać regułę wybierania λ
Pozostaje wyjaśnić sposób wyboru kierunku losowego po rozproszeniu
neutronu. Ponieważ problem posiada pełną symetrię względem osi
x, to kierunek w zupełności określa podanie jednego tylko kąta
między kierunkiem prędkości neutronu i osią Ox. Można pokazać,
że żądanie jednakowego prawdopodobieństwa kierunku rozpraszenia
jest równoważne żądaniu by cosinus kąta, μ = cosϕ, miał
rozkład jednorodny w przedziale (−1,1). Z (24) wynika, że dla
a=−1, b=1 formuła losowania μ jest:
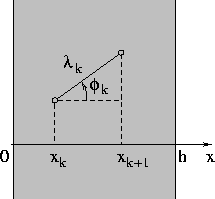
7.2. Schemat obliczeń nz bazie modelowania rzeczywistych
dróg. Załóżmy, że neutron uległ k-temu rozproszeniu w punkcie
o rzędnej xk wewnątrz płytki i następnie, porusza się
w kierunku μk. Wylosujmy drogę swobodną
i wyliczmy rzędną następnego zderzenia (rys. 23)
Sprawdzamy warunek przejścia przez płytkę
Jeżeli jest on spełniony, kończymy obliczenia dla tej trajektorii
neutronu i dodajemy jedynkę do licznika cząstek, które przeszły
przez płytkę. W przeciwnym przypadku, sprawdzamy warunek odbicia:
Jeśli jest on spełniony, to dodajemy jedynkę do licznika cząstek
odbitych. W wypadku, gdy warunek ten nie jest spełniony, tzn.
0 ≤ xk+1 ≤ h,
neutron doznał k+1 zderzenia wewnątrz płytki
i należy wylosować zachowanie się neutronu po zderzeniu.
Zgodnie z p. 4.1 wybieramy kolejną wartość γ i sprawdzamy
warunek wychwytu:
Jeżeli ostatni warunek jest spełniony należy zakończyć
rachunek dla tej trajektorii należy zakończyć dodaniem do licznika
pochłoniętych neutronów jedynki. W przypadku niespełnienia warunku,
uważamy, że neutron uległ rozproszeniu w punkcie, którego rzędna
wynosi xk+1. Rozgrywamy wówczas nowy kierunek prędkości
neutronu
i powtarzamy cały cykl od początku (oczywiście z innymi tym razem
wartościami γ)
Wszystkie γ wypisane zostały bez wskaźników, gdyż
pamiętamy, że każdej wartości γ używamy tylko raz.
Dla obliczenia jednego ogniwa trajektorii potrzebne są trzy wartości
γ. Początek każdej trajektorii zadany jest przez:
Po obliczeniach przeprowadzonych dla N trajektorii okaże się, że
N+ neutronów przeszło przez płytkę, N− neutronów uległo
odbiciu, a N0 zostało pochłoniętych w płytce. Poszukiwane
prawdopodobieństwa są wię dane przez
|
p+= |
N+
N
|
, p−= |
N−
N
|
, p0= |
N0
N
|
. |
|
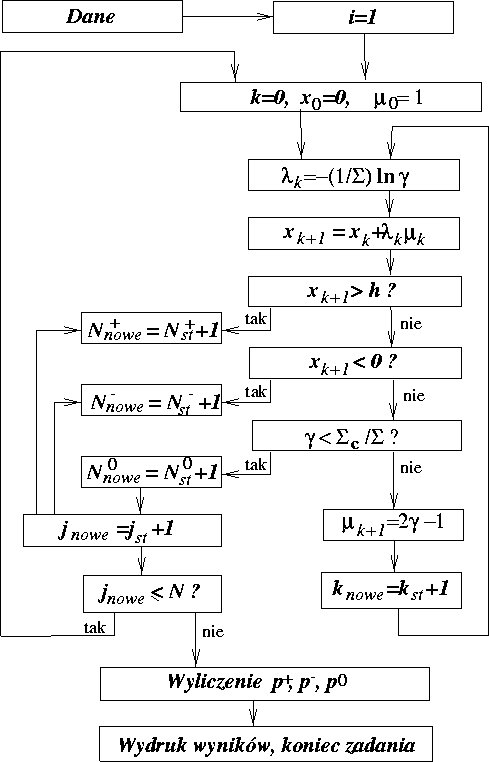
Na rys. 24 pokazano schemat blokowy programu obliczeń. Wskaźnik
j jest numerem trajektorii, wskażnik k - numer zderzenia
(na trajektorii).
Taka metodyka obliczeń jest bardzo naturalna lecz nie jest doskonała.
W szczególności, metoda ta nie nadaje się do obliczeń
prawdopodobieństwa p+, gdy jest ono bardzo małe. Z takim przypadkiem
spotykamy się akurat przy obliczeniach dotyczących ochrony przed
promieniowaniem.
Istnieją bardziej pomysłowe odmiany metody Monte Carlo, pozwalające
prowadzić obliczenia i dla takich przypadków. Zatrzymamy się na
krótko nad jednym z prostszych wariantów obliczeń z wykorzystaniem
tak zwanych wag.
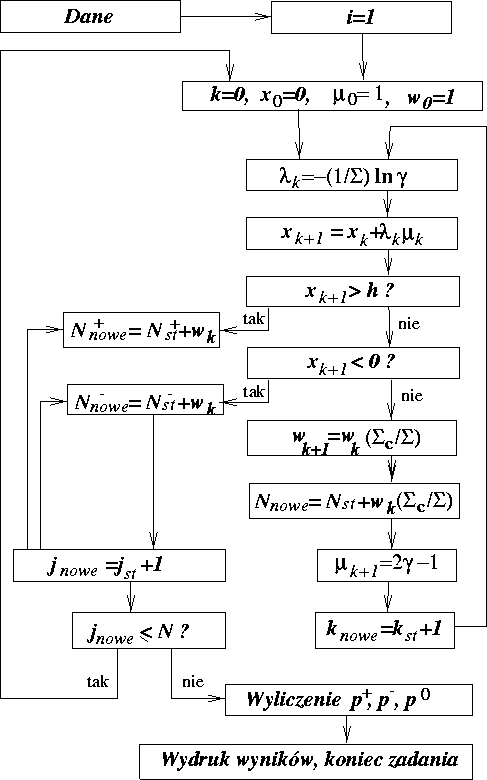
7.3. Schemat obliczeń z wykorzystaniem wag, zastępujących
pochłanianie.
Rozpatrzymy ten sam problem przechodzenia neutronów. Założymy, że
wzdłuż tej samej trajektorii porusza sie strumień złożony
z dużej liczby w0 jednakowych neutronów. Przy zderzeniu w punkcie
o rzędnej x1 średnia liczba pochłoniętych neutronów jest
równa w0(Σc//Σ, a srednia liczba neutronów
rozproszonych jest równa w0(Σs//Σ. Dodajemy liczbę
w0(Σc//Σ do licznika cząstek pochłoniętych, a ruch
strumienia rozproszonego będziemy obserwować dalej zakładając, że
pozostała część strumienia uległa rozproszeniu w tym samym
kierunku.
Wszystkie formuły, podane w poprzednim punkcie, pozostają bez zmian.
Jedynie liczba neutronów w paczce będzie się zmniejszać
gdyż część strumienia ,
zawierająca wk(Σc//Σ) neutronów, zostanie
pochłonięta. Teraz, trajektoria nie może zakończyć się
całkowitym pochłanianiem.
Wielkość wk nazywa się zazwyczaj wagą neutronu i zamiast
mówić o paczce złożonej z wk neutronów mówi się o jednym
neutronie z wagą wk. Początkową wagę przyjmuje się równą 1. Nie
przeczy to założeniu o dużej paczce , gdyż jak łatwo
zauważyć, wszystkie wk otrzymane przy obliczeniach dla jednej
trajektorii, zawierają wspólny czynnik w0.
Schemat blokowy programu takich obliczeń przedstawiony jest na rys.
25. Jego złożoność nie jest wcale większa niż złożoność
schematu z rys. 24. Można jednakże pokazać, że obliczenia tą
metodą są o wiele dokładniejsze niż obliczenia wykonane metodą
imitacji.
Uwagi.
Istnieje wiele rozmaitych metod obliczeń wykorzystujących różne
wagi. Nie będziemy ich dyskutować. Zauważymy jedynie, że metoda
Monte Carlo pozwala rozwiązywać bardziej skomplikowane problemy
z dziedziny cząstek elementarnych. Badany materiał może składać
się z różnych substancji i posiadać dowolną strukturę
geometryczną. Energia cząstek przy każdym zderzeniu może się
zmieniać. Można rozpatrywać wiele innych procesów jądrowych (na
przykład możliwość rozszczepienia jądra przy zderzeniu z neutronem
i powstawanie w tym procesie nowych neutronów). Można rozważać
warunki zachodzenia kontrolowanej reakcji łańcuchowej, itd (patrz
§8).
7 §8. Problem astrofizyczny
W charakterze realnego problemu, rozwiązanego metodą Monte Carlo,
pokażemy przykład, który w jakimś stopniu przystaje do § 7: tutaj
również rozpatruje się przechodzenie cząstek przez materię.
Cząstkami są nie neutrony, lecz fotony - najmniejsze cząstki
światła. Zamiast zwykłej płytki mamy sferyczny obłok
plazmy.2
Komptonizacja. Po odkryciu rozbłysków promieni
rentgenowskich i rozbłysków promieniowania gamma pochodzenia
kosmicznego, astrofizycy zaczęli poświęcać dużo uwagi budowie
modeli, które mogłyby wyjaśnić obserwowane widma promieniowania:
potęgowy charakter wielu widm wydawał się początkowo trudny do
wyjaśnienia.
Najprostszy model zwartego źródła to obłok gorącej plazmy,
w którego środku powstają fotony o niskiej częstości.
Rozpraszając się wielokrotnie na gorących elektronach plazmy, fotony
powiększają swoją energię hν i opuszczają obłok jako twarde
promieniowanie rentgenowskie lub gamma.
Jak wiemy, zmiana energii fotonu w procesie rozpraszania na elektronie
nosi nazwę efektu Comptona. Z tego powodu opisany wyżej proces
nazywa się komptonizacją. Komptonizacja pozwala wyjaśnić
obserwowane widma promieniowania gwiazd neutronowych, jąder
galaktycznych, kwazarów, dysków akrecyjnych powstałych w pobliżu
czarnych dziur. Nadzwyczaj efektywną metodą obliczeń komptonizacji
okazała się być metoda Monte Carlo.
(W rzeczywistości fotony nie muszą powstawać w centrum obłoku:
może tam na przykład, znajdować się czarna dziura. Obliczenia
pokazały, że kształt widma promieniowania wychodzącego z obłoku,
przy dużych hν nie zależy od miejsca powstawania fotonów
wewnątrz chmury. Jak mówią fizycy, foton, który rozprasza sie
wielokrotnie, zapomina o miejscu swoich urodzin...)
8.2. Konkretny przykład. Rys. 26, zapożyczony z cytowanej
wcześniej pracy, przedstawia próbę modelowania widma promieniowania
jądra galaktyki Seyferta NGC 4151. Wielkość strumienia fotonów
Fν, który przedstawia oś pionowa, jest proporcjonalna do
prawdopodobieństwa wylotu fotonu o energii hν. Punkty
reprezentują dane eksperymentalne; błędy danych, niekiedy całkiem
duże, nie zostały pokazane.
Histogram na rys. 26 otrzymano metodą Monte Carlo: przyjęto, że
częstościowy rozkład powstających fotonów ma charakter planckowski
z temperaturą Tr, a rozkład prędkości elektronów jest
maxwellowski z temperaturą Te. Wartości liczbowe: kTr=0.5 eV,
kTe=2 MeV, promień chmury równa się 0.4 średniej drogi swobodnej
fotonu, względem zimnych elektronów.
Z rys. 26 wynika, że w całkiem dużym przedziale energii,
w przybliżeni od hν = 0.1 MeV do hν = 6 MeV, wielkość logFν jest proporcjonalna do loghν. Z wielkości nachylenia
histogramu na tym odcinku można oszacować współczynnik kątowy
prostej przybliżającej dane i stwierdzić, że
Przy dalszym zwiększaniu się hν charakter widma zmienia się:
zaznacza sią eksponencjalny zanik.
8.3. O metodyce obliczeń.
Jak wspomnieliśmy wcześniej, przechodzenie fotonów przez obłok
można modelować tak jak zrobiliśmy to w §7. Energię każdego
powstającego fotonu należy wybrać zgodnie z rozkładem Plancka.
Prędkość rozpraszających elektronów również należy losować.
Za każdym razem trzeba będzie obliczyć średnią drogę swobodną
fotonu gdyż zależy ona od hν itd. Wypisywanie formuł
obliczeniowych nie jest chyba celowe.
O wiele ciekawiej jest zauważyć, że prawdopodobieństwa w prawej
części widma (patrz rys. 26) są 106 razy mniejsze niż w prawej.
Drogą modelowania imitacyjnego nie da się tego wyliczyć. Faktycznie,
histogram na rys. 26 otrzymany został tylko dzięki wykorzystaniu wag.
Było to o wiele bardziej skomplikowane niż opisano w §7.3:
w przypadku fotonu o wadze wk po k-tym rozproszeniu, wyliczano
prawdopodobieństwo bezpośredniej ucieczki Lk; część fotonu
z wagą wkLk dodawano do licznika ucieczek, a w przypadku
pozostałej części z wagą wk+1=wk(1−Lk) losowano k+1-szy
akt rozpraszania.
Przypisy:
1W ogólności, gęstość p(x) może
znikać [patrz notka w p. 2.2], lecz tylko w tych punktach, w których
g(x)=0.
2Pozdnyakov, L.A., Sobol, I.M., Sunyaev, R.A.,
Komptonizacja i tworzenie się widm źródeł rentgenowskich. Metodyka
obliczeń metodą Monte Carlo. Itogi Nauki i Techniki WINITI AN SSSR, Ser.
Astronomia, 1981, 21.
Bardziej kompletny wariant został opublikowany w: Pozdnyakov, L.A.,
Sobol, I.M., Sunyaev, R.A., Comptonization and the shaping of
X-ray source spectra: Monte Carlo calculations. -In: Soviet
scientific reviews.
Sect. E: Astrophys. and space phys. revievs. Harwood Acad. Publishers,
1983, 2, p. 189-331.
File translated from
TEX
by
TTH,
version 4.08.
On 27 Oct 2016, 21:01.