Temat: Potencjał. Linie sił pola elektrycznego. Transformacje konforemne.
Na podstawie: ...
1 Wstęga o zadanym potencjale. Linie ekwipotencjalne. Linie sił
P r o b l e m.
Znaleźć linie ekwipotencjalne w przypadku wstęgi o zadanym potencjale
położonej na płaszczyźnie uziemionej i linie sił pola.
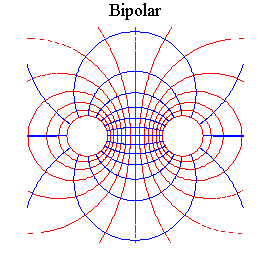
Najlepiej jest (?) pracować we współrzędnych bipolarnych zadanych
następująco:
|
x= |
a sinh(v)
cosh(v)−cos(u)
|
, y= |
asin(u)
cosh(v)−cos(u)
|
|
| (1) |
gdzie
Wstęgę umieścimy tak by pokryła się z osią z. (Patrz rysunek; a=1).
Równanie Laplace'a redukuje się w tym wypadku do postaci
|
∆V(u,v) = |
∂2 V
∂u2
|
+ |
∂2V
∂v2
|
=0 . |
| (3) |
Jego rozwiązanie z zerową stałą separacji jest
|
V(u,v) = a u v + b u + c v + d . |
| (4) |
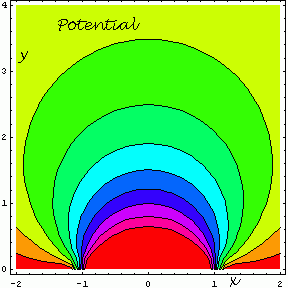
Z warunków brzegowych: V=0 dla x < −1 i x > 1 oraz V=V0 dla x ∈ < −1,1 >
dostaniemy a=c=d=0, b=V0/π.
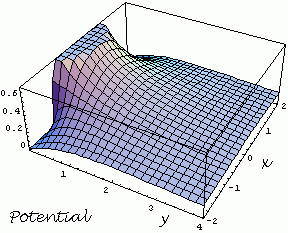
Otrzymane rozwiązanie we współrzędnych [x,y] przedstawiają rysunki.
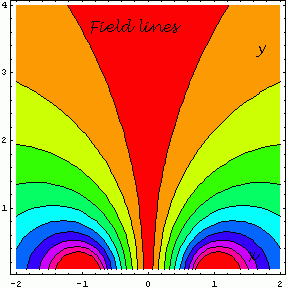
Linie sił pola v ∼ const przedstawia następny rysunek.
Związek pomiędzy współrzędnymi kartezjańskimi i bipolarnymi można odwrócić.
Dostaniemy