Zagadnienia egzaminacyjne z elektrodynamiki
dla studentów III roku fizyki
  1. Scharakteryzuj podstawowe oddziaływania w przyrodzie. Wprowadź pojęcie pola. Podaj klasyfikacje różnych działów elektrodynamiki.

  2. Zdefiniuj podstawowe wielkości w elektrodynamice, takie jak: prąd, gęstość prądu, ładunek, gęstość ładunku, siła elektromotoryczna, wektory natężeń i indukcji elektrycznej i magnetycznej, strumienie indukcji, ... , oraz podaj ich jednostki.

  3. Wychodząc z doświadczalnych praw: Faraday'a, Gaussa, Oersteda i prawa zachowania ładunku, wyprowadź równania Maxwella.

  4. Związek funkcji pola elektromagnetycznego z potencjałem skalarnym i wektorowym.

  5. Równania d'Alemberta dla potencjałów skalarnego i wektorowego.

  6. Transformacja cechowania potencjałów pola elektromagnetycznego i warunek Lorentza.

  7. Uzasadnij postulat o niezmienniczości interwału czasoprzestrzennego i podaj szczególną transformację Lorentza łączącą dwa różne układy inercjalne w przestrzeni czterowymiarowej.

  8. Czterowektory potencjału, gęstości prądu i równania d'Alemberta w przestrzeni czterowymiarowej.

  9. Cztero-tensor pola elektromagnetycznego i związek jego składowych z wektorami natężenia pola elektrycznego i indukcji magnetycznej.

  10. Wykaż, że równania Maxwella dla pól elektromagnetycznych są niezmiennicze ze względu na transformację Lorentza.

  11. Potencjały pochodzące od poruszających się ładunków (Lienarda - Wiecherta).

  12. Wychodzac z relatywistycznej zasady najmniejszego działania dla cząstki w polu elektromagnetycznym wyprowadź wzór na siłę Lorentza.

  13. Wychodząc z relatywistycznej zasady najmniejszego działania wyprowadź wzór na funkcje Hamiltona (energii) pola elektromagnetycznego.

  14. Uśredniając mikroskopowe pola elektromagnetyczne wyprowadź równania Maxwella w ośrodkach materialnych.

  15. Wychodząc z różniczkowego prawa Ohma wyprowadź znane prawo Ohma dla przewodników liniowych.

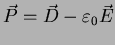  16. Wykaż, że wektor elektrycznej polaryzacji ośrodka $\vec P = \vec D - \varepsilon_0 \vec E$ jest wektorem gęstości momentu dipolowego ładunków związanych.

  17. Wykaż, że wektor magnetycznej polaryzacji ośrodka (magnetyzacji) 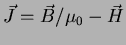$\vec J = {\vec B}/{\mu_0} - \vec H$ jest wektorem gęstości momentu dipolowego prądów związanych.

  18. Omów linie sił pola elektrycznego i magnetycznego i wykaż dlaczego załamują się one na granicy dwóch ośrodków.

  19. Wychodząc ze wzoru na gęstość siły Lorentza wyprowadź lokalne, różniczkowe prawo zachowania energii.

  20. Wyprowadź wzór na gęstość energii pola elektromagnetycznego i na wektor Poytinga (strumienia gęstości energii pola e.m.).

  21. Wyprowadź równanie Poissona dla potencjału skalarnego i podaj jego rozwiązanie dla ładunku punktowego.

  22. Podaj rozwiązanie równania Poissona dla ciągłego rozkładu ładunków (objętościowych, powierzchniowych i liniowych).

  23. Skalarny potencjał i nateżenie pola elektrycznego pochodzące od dipola.

  24. Potencjał elektryczny pochodzacy od naładowanej różnoimiennie warstwy podwójnej.

  25. Rozwinięcie multipolowe potencjału pochodzącego od objętościowego rozkładu ładunków.

  26. Własności przewodników w polu elektrostatycznym.

  27. Udowodnij prawdziwość twierdzenia o jednoznaczności rozwiazań równań elektrostatyki.

  28. Korzystajac z wzorów Greena wyprowadź wzór na potencjał pola elektrostatycznego pochodzący od objętościowego i powierzchniowego rozkładu ładunków i od warstwy podwójnej.

  29. Omów metodę rozwiązywania równania Laplace'a przy pomocy rozdzielania zmiennych. Podaj przykład rozwiazania w zmiennych x,y,z.

  30. Omów metodę rozwiązywania równania Laplace'a dla układów o symetrii osiowej.

  31. Omów metodę rozwiązywania równania Laplace'a dla układów o symetrii sferycznej.

  32. Wspołczynniki indukcji elektrostatycznej i pojemności układu n przewodników.

  33. Wyprowadź wzór na pojemność kondensatora kulistego, cylindrycznego i płaskiego.

  34. Wyprowadź wzór na energie układu ładunków w elektrostatyce.

  35. Oblicz energię elektrostatyczną jednorodnie naładowanej kuli i porównaj ją z energia kuli metalowej o takim samym promieniu i zgromadzonym na niej ładunku.

  36. Wyprowadź wzór na energię oddziaływania elektrostatycznego dwóch dipoli.

  37. Udowodnij prawdziwość twierdzenia Thomsona o energii układu ładunków rozłożonych na powierzchniach zamkniętych.

  38. Wychodząc z zasady zachowania energii wyprowadź wzór na gęstość siły objętościowej działajacej na substancję w polu elektrostatycznym.

  39. Tensor napięć Maxwella i jego zwiazek z gestościa siły działajacej na dielektryki w stałym polu elektrycznym.

  40. Wyprowadź równanie d'Alemberta dla potencjału wektorowego pochodzącego od prądów stacjonarnych.

  41. Potencjał wektorowy i pole magnetyczne pochodzące od przewodników liniowych.

  42. Potencjał wektorowy i pole magnetyczne na dużych odległościach od obszarów z prądem (przybliżenie dipolowe).

  43. Wychodzac ze wzoru na gęstość energii pola elektromagnetycznego wyprowadź wzór na energię układu prądów.

  44. Współczynniki indukcji wzajemnej i samoindukcji dla układu przewodników liniowych.

  45. Wyprowadź związek między strumieniem indukcji magnetycznej a natężeniami prądów płynących w układzie przewodników liniowych.

  46. Wyznacz współczynnik samoindukcji dla dowolnie wybranego selenoidu.

  47. Wychodząc z wzoru Lorentza i prawa Biota-Savarta wyprowadź wzór na siłę działającą między przewodnikami liniowymi z pradem.

  48. Wychodząc z równań Maxwella wyprowadź prawa Kirchhoffa dla prądów kwaziliniowych.

  49. Wychodząc ze wzoru na gestość siły Lorentza wyprowadź wzór Joule'a - Lentza na ilość ciepła wydzielaną w przewodniku z prądem.

  50. Wykaż, ze prądy szybkozmienne płyną głównie w warstwie powierzchniowej przewodnika.

  51. Wyprowadź podstawowe równanie opisujące przebieg prądów w obwodach złożonych z opornika, indukcyjności i pojemności.

  52. Znajdź przebieg prądu w obwodzie złożonym z indukcyjnosci i oporności w którym w chwili początkowej: a) płynie prąd o zadanym natężeniu, b) włączono stałą siłę elektromotoryczną.

  53. Znajdź przebieg czasowy natężenia prądu w pojedynczym obwodzie złozonym z oporności, indukcyjności i pojemności w którym w chwili poczatkowej jest zadany ładunek elektryczny na kondensatorze.

  54. Opisz przebieg prądu w obwodzie złożonym z oporności, indukcyjnosci i pojemności do którego przyłożono zewnetrzną, harmoniczną siłę elektromotoryczną.

  55. Drgania w sprzężonych indukcyjnie obwodach pradu kwazistacjonarnego.

  56. Znajdź rozwiązania równań d'Alemberta w postaci potencjałów opóźnionych i przedwczesnych.

  57. Wychodzac z równań Maxwella wyprowadź równania falowe dla pola elekrycznego i magnetycznego. Dowiedź, że oba pola są ze sobą sprzężone.

  58. Omów podstawowe własności rozwiązania równania falowego w postaci płaskiej fali elektromagnetycznej.

  59. Wyznacz gęstość energii i wektor strumienia energii (Poytinga) dla fali elektromagnetycznej.

  60. Polaryzacja liniowa, kołowa i eliptyczna fali elektromagnetycznej.

  61. Czterowektor falowy i relatywistyczny efekt Dopplera.

  62. Rozchodzenie się fal elektromagnetycznych w ośrodku przewodzącym.

  63. Odbicie i załamanie się fali elektromagnetycznej na granicy dwóch ośrodków. Prawa Snella.

  64. Związki między amplitudami fal elektromagnetycznych: padającej, odbitej i załamanej na granicy dwóch ośrodków (wzory Fresnela).

  65. Polaryzacja odbitej od granicy dwóch ośrodków fali elektromagnetycznej. Kąt Brewstera.

  66. Pokaż kiedy zachodzi całkowite wewnętrzne odbicie fali elektromagnetycznej od granicy dwóch ośrodków.

  67. Współczynniki transmisji i odbicia fali elektromagnetycznej od granicy dwóch ośrodków.

  68. Stojąca fala elektromagnetyczna w prostopadłościennym rezonatorze.

  69. Rozchodzenie sie fal elektromagnetycznych w falowodach. Fale transwersalne magnetyczne i transwersalne elektryczne. Prędkość grupowa i prędkość fazowa fal w falowodach.

  70. Rozchodzenie się fal elektromagnetycznych w ośrodkach anizotropowych (kryształach). Promień zwyczajny i nadzwyczajny.

  71. Rozwiązanie równań d'Alemberta dla potencjałów wektorowego i skalarnego przy pomocy wektora Hertza.

  72. Promieniowanie elektromagnetyczne wysyłane przez dipol Hertza.

  73. Promieniowanie hamowania w przybliżeniu dipolowym.

  74. Promieniowanie elektromagnetyczne wysyłane przez antenę liniową.

  75. Dyspersja fal elektromagnetycznych w ośrodkach.







2009-04-26