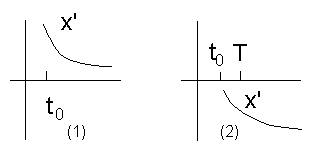Podstawa: Bogdanow, Serojad
1 Oscylacje rozwiązań liniowych równań różniczkowych
Zajmiemy się liniowym równaniem skalarnym drugiego rzędu
|
y"(t) + p(t) y′(t) +q(t) y(t) = 0 , t ∈ I = [a, b] , |
| (1) |
gdzie funkcje p i q są ciągłe na I.
Z twierdzenia o jednoznaczności rozwiązania wynika, że każdy problem
Cauchy'ego (1) posiada jednoznaczne rozwiązanie na I.
W szczególności, jeśli rozwiązanie zeruje się wraz z pochodną
w jakimś punkcie w I to jest to rozwiązanie zerowe. Dalej zakłada się,
że rozwiązanie równania (1) jest niezerowe.
Jeżeli więc rozwiązanie y jest zerem w t0 ∈ I to y′(t0) ≠ 0
i w rezultacie w punkcie wewnętrznym t0 ∈ I rozwiązanie zmienia znak
przy przechodzeniu przez t0, a więc jego wykres przecina oś x.
1.1 Zera rozwiązania
Lemat 1
Żadne z niezerowych rozwiązań równania (1) nie posiada
nieskończonej liczby zer na dowolnym przedziale [α, β] ∈ I,
a więc zera dowolnego rozwiązania są izolowane.
° Jeśli y posiada nieskończenie wiele zer na przedziale [α, β] ∈ I
to w punkcie granicznym (skupienia) zbioru zer mamy)
i wobec tego rozwiązanie jest zerowe co jest sprzeczne z założeniem.
Zera są więc izolowane.°
1.2 Niezależność liniowa
Lemat 2 Jeśli dwa rozwiązania równania (1) lub ich pierwsze
pochodne znikają w jakimś punkcie odcinka I to rozwiązania te są liniowo
zależne, tzn. różnią się stałym czynnikiem.
° Wrońskian w rozwiązań y1 i y2 jest równy w = y1y′2−y2y′1.
Z założenia, w którymś punkcie t0 ∈ I, w(t0)=0. Z formuły Liouville'a
wynika, że w(t)=0 ∀t ∈ I. Oznacza to, że rozwiązania są liniowo
zależne.°
Definicja 1
Rozwiązanie równania (1) nazywa sie nieoscylującym na przedziale
I1 ⊂ I jeśli posiada na I1 nie więcej niż jedno zero. W przeciwnym
wypadku rozwiązanie nazywa się oscylującym.
P r z y k ł a d 1.
Rozwiązanie równania
jest nieoscylujące na przedziale I=(−∞, +∞) gdyż jest postaci
y(t) = c
1e
ωt + c
2e
−ωt.
P r z y k ł a d 2.
Ogólne rozwiązanie równania
jest postaci y(t) = A sin(ωt + ϕ) i stąd, odległość między
zerami y(t) jest równa π/ω. Na dowolnym odcinku o długości
mniejszej niż π/ω rozwiązania są nieoscylujące, a na dłuższych
odcinkach są oscylujące.
1.3 Wskaźnik braku oscylacji rozwiązań
Lemat 3
Każde rozwiązanie (1) jest nieoscylujące na I1 ⊂ I jeżeli
na I1 funkcja q(t) ≤ 0.
° Niech y będzie dowolnym rozwiązaniem równania (1).
Zbadamy funkcję
|
h(t) ≡ exp[ | ⌠
⌡
|
t
s
|
p(τ)dτ]·y(t) y′(t) , |
| (5) |
gdzie s jest punktem początkowym na I.
|
h′(t) = exp[ | ⌠
⌡
|
t
s
|
pdτ]·[(y′(t)2 − q(t) y2(t)] . |
| (6) |
Z założenia wynilka, że h′(t) ≥ 0 dla wszystkich t ∈ I1.
W rezultacie, funkcja h(t) rośnie (słabo) na I1. Jeśli istniałyby
dwa punkty t1, t2 ∈ I1 i t1 < t2 takie, że y(t1) = y(t2) = 0,
to h(t) = 0 dla wszystkich t ∈ [t1, t2]. Stąd wynikałoby, że
y(t) y′(t) = 0 ∀t ∈ [t1, t2]. Na podstawie lematu o zerach
rozwiązanie y może posiadać na [t1, t2] tylko izolowane zera.
Stąd
|
y′(t) = 0, ∀t ∈ [t1, t2] → y(t) = 0, ∀t ∈ [t1, t2] , |
| (7) |
tzn. rozwiązanie y jest zerowe!? Otrzymana sprzeczność pokazuje, że
rozwiązanie y posiada nie więcej niż jedno zero na I1, jest to więc
rozwiązanie nieoscylujące.°
P r z y k ł a d 3.
Rozwiązanie równania Eulera
|
t2 y" + t a1 y′+ a0 y = 0 , t > 0 |
| (8) |
jest nieoscylujące jeśli a
0 ≤ 0.
1.4 Postać kanoniczna równania drugiego rzędu
Jeśli w równaniu
|
y"(t) + p(t) y′(t) +q(t) y(t) = 0 , t ∈ I = [a, b] , |
| (9) |
wykonamy podstawienie
to dostaniemy
|
u" z + 2 u′z′+ u z" + p (u′z + u z′) + q u z = 0 |
| (11) |
i dalej
|
u z" + (2 u′+ p u) z′+ (u" + pu′+ q u) z = 0 . |
| (12) |
Wybierzemy u tak by
i założymy, że p(t) ∈ C1. Równanie to spełnia funkcja
|
u(t) = e−1/2∫t0t p(τ)dτ . |
| (14) |
Mamy więc
|
u"+pu′+pu=... = u ( |
p2
4
|
− |
p′
2
|
+ q) |
| (15) |
Ponieważ u ≠ 0 więc dostaniemy
|
z" + Q(t) z = 0 , Q = |
p2
4
|
− |
p′
2
|
+ q . |
| (16) |
Ta postać równania drugiego rzędu nosi nazwę postaci kanonicznej.
P r z y k ł a d 4.
Równanie Bessela
|
x2 y" + x y′+ (x2 − n2) y = 0 , x > 0 |
| (17) |
po zamianie zmiennej y=x
−1/2z prowadzi do postaci kanonicznej
|
z" + (1 − |
n2−1/4
x2
|
) z = 0 . |
| (18) |
(Tutaj p=1/x, q=(x
2−n
2)/x
2. Stąd Q=1−(n
2−1/4)/x
2. Dalej
e
−1/2∫(1/x) dx = e
−1/2lnx = x
−1/2. Więc y = z x
−1/2)
1.5 Twierdzenie Sturma o porównaniach
Niech będą dane dwa równania w postaci kanonicznej:
o współczynnikach (Q, R) ciągłych na I.
Twierdzenie 1
Jeśli t1 i t2, t1 < t2 są zerami rozwiązania równania (19)
oraz
|
Q(t) ≤ R(t) , ∀t ∈ [t1, t2] |
| (21) |
to dowolne rozwiązanie y równania (20) na odcinku [t1, t2]
posiada co najmniej jedno zero. Jeśli w dodatku t1 i t2 nie są
jednocześnie zerami rozwiązania y, to y posiada zero w przedziale
(t1, t2).
° Niech y będzie dowolnym rozwiązaniem równania (20).
Wstawmy y i x do odpowiednich równań. Otrzymane tożsamości
pomnóżmy przez y i x odpowiednio i odejmijmy drugą z nich od pierwszej.
Dostaniemy
|
x"(t) y(t) − y"(t)x(t) + (Q(t)−R(t)) x(t) y(t) = 0 |
| (22) |
lub
|
|
d
dt
|
[x′y−y′x] = [R(t)−Q(t)]xy . |
| (23) |
Całkując po t od t1 do t2 i wykorzystując warunek
otrzymamy
|
x′(t2) y(t2) − x′(t1) y(t1) = | ⌠
⌡
|
t2
t1
|
(R−Q)x y dt . |
| (25) |
Przyjmiemy dalej , że t1 i t2 są kolejnymi zerami rozwiązania x.
Wobec tego x na przedziale (t1, t2) ma jednakowy znak. Ustalmy, że x(t) > 0, ∀t ∈ (t1, t2) Ponieważ x′(t1) ≠ 0 i x′(t2) ≠ 0
to x′(t1) > 0 i x′(t2) < 0.
Założenie, że rozwiązanie y nie znika na przedziale (t1, t2) jak
również na jednym z jego końców prowadzi do sprzeczności z równością
(25). Jeśli bowiem y > 0 (y < 0) to lewa strona (25) jest
ujemna (dodatnia) a prawa jest nieujemna (niedodatnia). Wobec tego każde
rozwiązanie równania (20) posiada co najmniej jedno zero na [t1, t2].
Jeśli rozwiązanie nie zeruje się na końcach przedziału to posiada zero
w przedziale otwartym (t1, t2).°
Zauważmy, że jeśli (21) jest silną nierównością przynajmniej
w jednym punkcie, to równanie (20) posiada zero w przedziale (t1, t2)
(wynika to z równania (25)) oraz własności silnej monotoniczności
całki).
Wniosek 1
Każde rozwiązanie równania (19) jest nieoscylujące na przedziale
I jeśli Q(t) ≤ 0 na I.
° Jeśli istniałoby rozwiązanie x znikające co najmniej w dwu punktach, to
z twierdzenia Sturma wynika, że każde z rozwiązań równania
powinno być zerem na I co jest fałszem bo istnieją rozwiązania (y = 1),
które nie posiadają zer na I.°
Wniosek 2
Zera liniowo niezależnych rozwiązań równania (19) wzajemnie sią
rozdzielają, tzn. między dwoma zerami jednego z rozwiązań istnieje
dokładine jedno zero drugiego rozwiązania.
° Niech x1 i x2 będą liniowo niezależnymi rozwiązaniami równania
(19). Z lematu o niezależności liniowej wynika, że nie mogą posiadać
one wspólnych zer. Z twierdzenia Sturma wynika, że między kolejnymi zerami
t1 i t2 rozwiązania x1 leży co noajmniej jedno zero rozwiązania x2.
Zamieniając miejscami x1 z x2 w przeprowadzonym rozumowaniu dochodzimy
do wniosku, że zera t1 i t2 rozwiązania x1 nie są kolejnymi
zerami.°
1.6 Przypadek nieskończonej liczby zer
Twierdzenie 2
Jeśli przedział I jest niewłaściwy i
to wszystkie rozwiązania równania (19) mają nieskończenie
wiele zer.
Dowód przeprowadzamy porównując (19) z równaniem x"+mx=0
i korzystając z wyników przykładu 2.
P r z y k ł a d 5.
Rozpatrzmy równanie Bessela w postaci kanonicznej
|
x" + ( 1 − |
n2−1/4
t2
|
) x = 0 , t > 0 . |
| (28) |
Dla 0 ≤ n ≤ 1/2 spełniona jest nierówność
i dlatego wszystkie rozwiązania równania Bessela posiadają
nieskończenie wiele zer. Odległość kolejnych zer jest w przypadku
0 ≤ n ≤ 1/2 mniejsza niż π. Przy n ≥ 1/2 istnieje również
nieskończona liczba zer, a ich odległość jest większa od π.
Ponieważ
to odległość zer dąży do π.
|
Q(t) ≥ 0 , | ⌠
⌡
|
+∞
|
Q(τ)dτ = 0 , |
| (31) |
to wszystkie rozwiązania równania (19) posiadają nieskończenia wiele
zer.
° Załóżmy, że istnieje rozwiązanie x, które nie posiada
nieskończonej liczby zer. Jstnieje wtedy taki punkt t0, że przy
t ≥ t0 funkcja x ma stały znak. Przyjmijmy
Ponieważ
|
x"(t) = −Q(t) x(t) , ∀t ≥ t0 , |
| (32) |
to x"(t) ≤ 0, i pochodna x′ maleje na przedziale
[t0, +∞]. Mamy dwie możliwości.
1o x′ ≥ 0 , ∀t ≥ t0. W tym przypadku x rośnie
ix(t) ≥ x(t0), ∀t ≥ t0. Całkując (32) w granicach
od t0 do t otrzymamy
|
x′(t) −x′(t0) = − | ⌠
⌡
|
t
t0
|
Q(s)ds ≤ −x(t0) | ⌠
⌡
|
t
t0
|
Q(s)ds , ∀t ≥ t0 |
|
|
x′(t0) ≥ x(t0) | ⌠
⌡
|
t
t0
|
Q(s)ds → ∞ przy t→+∞ |
|
Sprzeczność!
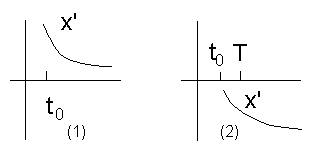
Pochodna x′(t)
2o x′(t) < 0 ∀t ≥ T , T > t0. Ponieważ x′ maleje, to
Stąd (po scałkowaniu od T do t) mamy
|
x(t) − x(T) ≤ x′(T) (t − T) , ∀t ≥ T , |
|
|
−x(T) ≤ x′(T) (t − T) → −∞ przy t→ +∞ . |
|
Otrzymane sprzeczności pokazują, że wszystkie rozwiązania równania
(19) posiadają nieskończenie wiele zer. °
P r z y k ł a d 6.
Wszystkie rozwiązania równania
|
x" + |
ω2
tα
|
x = 0, t > 0 , ω ≠ 0 |
|
dla α ≤ 1 posiadają nieskończenie wiele zer ponieważ
|
|
ω2
tα
|
>=0 dla t > 0 i | ⌠
⌡
|
+∞
|
|
ω2
tα
|
= ∞ . |
|
1.7 Dodatek. Wrońskian. Twierdzenie Liouville'a
1) Rozpatrzmy funkcje ψk , k=1,...,n na I ∈ R1 klasy Cn.
Wyznacznik
gdzie Dk=d/dtk, nazywa się wrońskianem (od nazwiska polskiego matematyka,
J. Wrońskiego). Wyliczymy Dw, biorąc pochodne z wyznacznika według wierszy
i odrzucając wyznaczniki o jednakowych wierszach
Rozpatrzmy równanie różniczkowe
gdzie operator Ln = Dn + an−1Dn−1 + ... + a1D1 + a0,
i współczynniki ak są stałe (operator Ln nazywa się wtedy stacjonarnym).
Lemat 4 (Liouville'a). Jeśli ψk są rozwiązaniami równania
gdzie Ln jest stacjonarny, to
° Funkcje ψk (rozwiązania równania) zamieniają (*) w tożsamość.
Dlatego
|
Dnψk = −an−1Dn−1ψk − ... − a1Dψk − a0ψk , ∀t . |
|
W wyniku (patrz równanie dla Dw) mamy
a to oznacza, że w(t) = w(0)exp(−an−1t). °
Twierdzenie 4
Rozwiązania ψk równania Ln x = 0 tworzą układ zupełny (bazę)
wtedy i tylko wtedy gdy w(t) ≠ 0 , ∀t.
° Zbudujmy ogólne rozwiązanie równania różniczkowego n−tego rzędu
Ln x = 0.
Utworzymy układ równań algebraicznych dla ck z pochodnych
w punkcie początkowym t=0
|
Dk x(0) = |
∑
l
|
clDkψlξk , k=0,...,n . |
| (u) |
Wyznacznikiem układu jest w(0). Jeśli w(0) ≠ 0 to układ (u) ma
jednoznaczne rozwiązania przy dowolnych ξk i dlatego ψk
tworzą bazę.
Odwrotnie, jeśli ψk tworzą bazę, to układ równań (u) można
rozwiązać dla dowolnych ξk, a stąd wynika, że w(0) ≠ 0,
co pociąga za sobą spełnienie nierówności w(t) ≠ 0, która wynika
z lematu Liouville'a (L). °
File translated from
TEX
by
TTH,
version 4.08.
On 23 Dec 2015, 13:49.