Podstawa: J.L. Quiroz Gonzáles, D. Thompson:
Getting started with Numerov Method,
Computers in Physics, 11, Sep/Oct 1997
1 Metoda Numerova
Równanie Schrödingera jest równaniem różniczkowym drugiego rzędu
i w wielu przypadkach nie zawiera pierwszej pochodnej. Prostą metodą
numeryczną rozwiązywania tego typu równań jest metoda Numerowa.
Metoda ta nosi też nazwę metody Numerova-Cowella-Goodwina-Foxa ....
Ogólniej, metoda służy ona do rozwiązywania równań typu
gdzie y=y(x). Do tej klasy równań, oprócz równania Schrödingera
zalicza się też równanie klasycznego, nie tłumionego oscylatora
harmonicznego
Prócz tego należy do niej równanie
Poissona opisujące potencjał w przypadku odpowiednio symetrycznego
rozkładu ładunku.
Metodę Numerowa można zastosować do równań, które nie posiadają
pierwszej pochodnej (patrz jednak Dodatek), a ich lewa
strona jest liniowa w y.
Aby otrzymać schemat różnicowy równania drugiegi rzędu
skorzystamy z definicji różnic centralnych.
Jeśli założymy, że współrzędna x została podzielona na
małe odcinki h i końce tych odcinków oznaczymy przez xn, natomiast
odpowiadające im wartości y(xn) oznaczymy przez yn, wówczas
korzystając z rozwinięcia y(x) w szereg Taylora, możemy zapisać
|
yn+1=yn + h |
dy
dx
|
+ |
h2
2!
|
|
d2y
dx2
|
+ |
h3
3!
|
|
d3
dx3
|
+ |
h4
4!
|
|
d4
dx4
|
+ ... |
| (4) |
Podobnie
|
yn−1=yn − h |
dy
dx
|
+ |
h2
2!
|
|
d2y
dx2
|
− |
h3
3!
|
|
d3
dx3
|
+ |
h4
4!
|
|
d4
dx4
|
+ ... |
| (5) |
Stąd dostaniemy
|
yn+1−2yn+yn−1 ≈ 2 | ⎛
⎝
|
h2
2!
|
|
d2y
dx2
|
+ |
h4
4!
|
|
d4y
dx4
|
+O(h6) | ⎞
⎠
|
. |
| (6) |
W celu ułatwienia zapisu oznaczymy prawą stronę równania (1)
przez
Składając równanie (1) i równanie (6) otrzymamy
|
yn+1=2yn−yn−1+h2Fn+ |
h4
12
|
|
d2F
dx2
|
+O(h6) . |
| (8) |
Zastąpimy teraz drugą pochodną F równaniem różnicowym podobnym do
równania (6), a więc
|
Fn+1−2Fn+Fn−1 ≈ 2 | ⎛
⎝
|
h2
2!
|
|
d2F
dx2
|
+ |
h4
4!
|
|
d4F
dx4
|
+O(h6) | ⎞
⎠
|
. |
| (9) |
W ten sposób otrzymamy różnicowy algorytm Numerowa całkowania
równania (1)
|
yn+1= |
2 yn−yn−1+h2/12 (Un+1+10 Fn + Fn−1)
(1 − Vn+1 h2/12)
|
+ O(h6) . |
| (10) |
Wykorzystaliśmy tutaj liniowość prawej strony równania (1)
w zmiennej zależnej y.
Na podstawie tego wzoru widzimy, że wykonanie jednego kroku całkowania
z dużą dokładnością, równą O(h6),
a więc wyliczenie kolejnego yn, wymaga tylko jednokrotnego wyznaczenia
funkcji U i V. Metoda Rungego-Kutty, w celu osiągnięcia tej samej
dokładności, potrzebuje obliczyć sześć wartości U i sześć wartości
V na jeden krok całkowania (patrz: Press, Teukolsky, Vetterling, Flannery,
Numerical Recipes, Cambridge UP, Cambridge, 1992.)
Z równania (10) widać, że dla wyznaczenia wartości
yn+1 potrzebujemy znać wartość y w dwu punktach poprzednich, a więc
yn i yn−1. Musimy więc zastanowić się jak rozpocząć obliczenia.
Zakładamy, że znamy wartość początkową y0=y(x0),
kt/ora pozwala obliczyć F0 i znamy pochodną y0′ (zagadnienie Cauchy).
Chcąc wyznaczyć y2 z dokładnością O(h6) musimy z taką dokładnością
znać y1. Okazuje się jednak, że wystarczy niższa dokładność obliczeń
y1, równa O(h5), a to z tego względu, iż błąd końcowy algorytmu
jest rzędu h5, a y1 wyznaczamy tylko raz.
Najlepsze co możemy zrobić to obliczyć y1 z rozwinięcia Taylora
|
y1=y0+hy0′+h2/2! F0+h3/3! F0′+ h4/4! F0" + O(h5) . |
| (11) |
Za pochodną F0′ wstawiamy
i obcinamy tak otrzymany szereg. Daje to
|
y1 = |
y0 + h y0′+ h2/6 (U1 − 2 F0)
1 − V1h2/6
|
+ O(h4) . |
| (13) |
Użycie tak wyliczonego y1 z dokładnością O(h4), może spowodować,
wzrost globalnego błędu obliczeń do O(h4)!
Z równania (11) widzimy, że w celu zmniejszenia błędu,
powinniśmy jak najdokładniej obliczyć drugą pochodną F0".
Niektórzy autorzy sugerują by zrobić to analitycznie co jednak nie zawsze
jest praktyczne. Inni proponują by obliczyć y1 z równania (11)
bez członów F0′ i F0" i następnie zastosować standardowy
algorytm Numerowa (1) w celu pierwszego oszacowania y2.
Wartość tę można następnie wykorzystać do wyznaczenia F0".
Powtarzając obliczenia, lecz już teraz z wykorzystaniem F0", można
uzyskać nowe wartości y1 i y2. Cykl obliczeń trwa do momentu gdy
obie wartości y1 i y2 przestaną się zmieniać. W tej sytuacji
przechodzimy do dalszych obliczeń według algorytmu Numerowa.
Jeszcze inna możliwość wyliczenia y1 polega na wykonaniu jednego
kroku całkowania z wykorzystaniem innego, samostartującego algorytmu
całkowania i następnie na przejściu do metody Numerowa.
Załóżmy tymczasem, że mamy pierwsze oszacowanie y1, które pozwoli
oszacować F2. Korzystając z F0, F1 i F2 możemy oszacować
F0" i stąd, z żądaną dokładnością, otrzymać y1.
Można powiedzieć, że poszukujemy y1 w postaci
|
y1 = y0 +h y0′+ h2 ( a F0 + b F1 + c F2 ) . |
| (14) |
Stałe a, b, c powinny być takie, by równania (11)
i (14) były ze sobą zgodne.
Uzyskamy je rozwijając F1 i F2 w szereg Taylora w punkcie x0.
| |
|
|
a F0 + b (F0 + h F0′+h2/2 F0" + ...) + c (F1 + h F1′+ h2/2 F1" + ...) |
| |
| |
|
| |
| |
|
| F0 ( a + b + c ) + F0′h ( b + 2 c ) + F0" h2/2 ( b + c + 3 c + c ) + ... |
| |
|
Porównując współczynniki tego rozwinięcia z odpowiadającymi im
współczynnikami w równaniu (11) dostaniemy
Stąd
|
a = 7/24, b=1/4, c = −1/24 . |
| (16) |
Możemy więc zapisać
| |
|
= y0 + h y0′+h2/24 ( 7 F0 + 6 F1 −F2 ) + O(h5) , |
| | (17) |
| |
| = |
2 y1 − y0 + h2/12 ( U2 + 10 F1 + F0 )
(1−V2 h2/12)
|
+ O(h5) . |
| | (18) |
|
Z dokładnością do członów O(h5) układ równań (18) jest
liniowy względem y1 i y2 (uwaga: y1 i y2 wchodzą do F1, F2).
|
a11 y1 + a12 y2 = b1; a21 y1 + a22 y2 = b2 . |
| (19) |
gdzie
| |
| | (20) |
| |
| | (21) |
| |
| | (22) |
| |
| | (23) |
| |
|
= y0 + h y0′+ h2 (7 F0 + 6 U1 − U2)/24 , |
| | (24) |
| |
| = −y0 +h2 ( F0 +10 U1 + U2 ) . |
| | (25) |
|
Stąd dostajemy y1 z błędem O(h5).
|
y1 = |
a22 b1 − a12 b2
a11 a22 − a12 a21
|
|
| (26) |
|
y1= |
y0(1−V2h2/24)+hy0′(1−V2h2/12)+h2/24(7F0+6U1−U2)−h4V2/36(F0+2U1)
1−V1 h2 / 4 + V1 V2 h4 / 18
|
. |
| (27) |
W pokazanej, ulepszonej metodzie Numerowa startujemy z równania (27)
i dalej korzystamy z równania (10).
Z a d a n i e 1.
Powtórzyć obliczenia prowadzące do wartości współczynników a, b, c
pokazanych w równaniu (16).
Z a d a n i e 2.
Napisać podprogram (Pascal, Fortran, c++) rozwiązywania równań
różniczkowych metodą Numerowa i wykonać test programu spradzając
w tym celu zgodność wyników numerycznych z rozwiązaniami analitycznymi
kilku znanych równań. Jak krok całkowania h wpływa na wyniki obliczeń?
Wykonać rysunki porównawcze rozwiązań dla trzech różnych kroków całkowania.
Z a d a n i e 3.
Rozwiązać równanie −0.5 y" + y + x = 0, y(0)=1, y′(0)=0, stosując
metodę Numerowa.
1.1 Dodatek. Użyteczna transformacja
Podstawa: Stephen B. Haley, An Underrated entanglement: Riccati and Schrödinger
equations, Am. J. Phys., 65, March 1997, pp237-243.
W takich sytuacjach jak np. elektron w polu magnetycznym, równanie Schrödingera
zawiera pierwszą pochodną. Zdarza się to również w innych przypadkach,
które prowadzą do równań drugiego rzędu. Rozpatrzmy równanie
|
|
d2Z
dx2
|
−2 a(x) |
dZ
dx
|
+b(x) Z(x) = 0 , |
| (28) |
w którym Z(x) jest nieznaną funkcją, a współczynniki a(x) i b(x)
są funkcjami x.
Pierwszą pochodną można wyeliminować wykonując transformację (patrz
np. Kamke)
|
Z(x) = Y(x) exp | ⎡
⎣
| ⌠
⌡
|
x
|
a(x′) dx′ | ⎤
⎦
|
. |
| (29) |
Prowadzi to do następującego równania dla Y(x)
gdzie
|
f(x) = |
da
dx
|
−a2(x) + b(x) . |
| (31) |
Podana transformacja jest częścią złożonej transformacji Liouville'a
używanej przez Berezina i Shubina do wyznaczenia asymptotycznych własności
funkcji własnych równania Schrödingera (patrz: F.A. Berezin, M.A. Shubin,
Urawnienie Schrödingera, Moskow, 1983.)
Postać (30) nosi nazwę postaci kanonicznej równania
różniczkowego drugiego rzędu (patrz następny rozdział).
Znalezienie transformacji odwrotnej, która pozwala otrzymać Z z zadanych
funkcji Y i f(x) wymaga rozwiązania równania Riccatiego
Szczególnym rozwiązaniem równania (
32), które jest transformacją
odwrotną jest
|
a(x) = i |
| ___
√ f(x)
|
, b(x) = − |
da
dx
|
. |
| (33) |
Ponieważ znamy zazwyczaj postać analityczną obu współczynników (chyba,
że mamy ich wartości numeryczne) to wykonanie podanej transformacji
(29) jest rzeczą prostą i możemy bezpośrednio stosować
metodę Numerowa do otrzymanego równania (30).
Z a d a n i e 4.
Rozwiązać równanie x3 y" = y [ y(1)=1, y′(1)=0 ] na odcinku (0,1〉.
Narysować wykres funkcji f(x)=y(x)/(x3/4 exp(2 x−1/2)).
Wynik powinien być podobny do przedstawionego na rysunku.
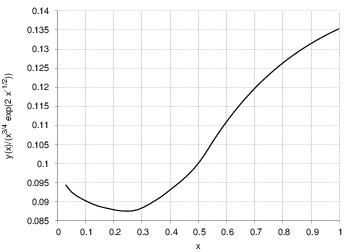
Wykres zależności
y(x)/(x
3/4 exp(2 x
−1/2))
gdzie y jest rozwiązaniem równania x
3y" = y [ y(1)=1, y′(1)=0]. Równanie rozwiązano metodą Numerova-Cowella, z krokiem h=0.0002.
Przykład programu
w Fortranie:
File translated from
TEX
by
TTH,
version 4.08.
On 13 Dec 2016, 16:25.


