1 Zachowanie się rozwiązań w otoczeniu NPO
Równanie
nie daje się rozwiązać metodą szeregów Frobeniusa.
Z a d a n i e 1.
Sprawdzić, że równanie x3 y" = y nie daje się rozwiązać metodą
szeregów Frobeniusa.
Każde równanie różniczkowe II rzędu ma dwa liniowo niezależne rozwiązania.
Opiszemy krótko procedurę, która pozwala znaleźć lokalne zachowanie rozwiązań
w pobliżu NPO. W przypadku równania (1) jest to punkt x=0.
Rozwiązanie jest
|
y(x) ∼ C1 x3/4 exp(2x−1/2) (x→ 0+) |
| (2) |
|
y(x)=C2 x3/4 exp(−2x−1/2) (x→ 0+) . |
| (3) |
Zauważmy, że rozwiązania zawieraja funkcję wykładniczą z funkcji, która jest
osobliwa w nieregularnym punkcie osobliwym równania różniczkowego. Posiadają więc
istotne osobliwości w x=0.
Pierwszy krok w wyznaczeniu głównego zachowania się rozwiązania w okolicy
NPO polega na identyfikacji tzw. czynnika kontrolnego. Jest to najczęściej
exponenta. Sugeruje to następujące podstawienie (Carlini 1817, Liouville 1837
Green 1837):
Sprowadza to liniowe równanie różniczkowe n-tego rzędu do przybliżonego
równania 1-go rzędu dla S(x), które jest zazwyczaj słuszne w obszarze NPO.
W celu prześledzenia metody zastosujemy podstawienie (4)
dla znalezienia czynnika kontrolującego w rozwiązaniu równania
|
y" + p(x) y′+ q(x) y = 0 , |
| (5) |
w pobliżu nieregularnego punktu osobliwego x0.
Podstawmy y=expS. Mamy
|
S" + (S′)2+p(x) S′+ q(x) = 0 . |
| (6) |
Równanie to jest tak samo trudne jak równanie (5) lecz zazwyczaj
upraszcza się z powodu faktu, że w okolicy NPO
Załóżmy, że czynnik kontrolny rozwiązania jest postaci exp[−a(x−x0)−b],
gdzie b > 0 tak, że y(x) ma w pobliżu x0 istotną osobliwość. Mamy wtedy
(S′)2 ∼ a2b2(x−x0)−2b−2 i S" ∼ ab(b+1)(x−x0)−b−2 .
Założenie (7) jest więc słuszne bo b > 0. Zróżniczkowaliśmy tutaj
relację asymptotyczną. Procedura ta zostanie uprawomocniona później.
Asymptotyczne równanie różniczkowe
|
(S′)2 ∼ −p(x) S′− q(x) , x→ x0 , |
| (8) |
które otrzymuje sie po odrzuceniu S", łatwo rozwiązać. Rozwiązania
można następnie użyć do sprawdzenia relacji (7).
(Zauważmy, że przenieśliśmy dwa człony na prawą stronę równania (8)
po to by uniknąć stwierdzenia, że funkcja jest asymptotyczna z zerem.)
Istnieją przypadki gdy (7) nie zachodzi. Relacja ta nie jest
też spełniona w ZPO lub RPO.
P r z y k ł a d 1.
Czynnik kontrolujący w otoczeniu NPO w zerze. Weźmy równanie x
3 y" = y.
Znajdziemy czynnik kontrolujący w otoczeniu zera, które jest NPO równania.
Równanie (
8) jest
Mamy dwa możliwe rozwiązania: S′(x) ∼ ±x
−3/2 (x→ x
0), a stąd
|
S(x) ∼ ±2 x−1/2 , x→ x0+ . |
| (9) |
|
| ⌠
⌡
|
x
|
f(x) dx ∼ [a/(1−b)](x−x0)1−b , x→ x0 ; |
|
Jeśli b < 1 to
|
| ⌠
⌡
|
x
|
f(x) dx ∼ c (const) przy x→ x0 ; |
|
Jeśli b = 1
|
| ⌠
⌡
|
x
|
f(x) dx ∼ a ln|x−x0| , x→ x0 . |
|
P r z y k ł a d 2.
Zachowanie główne w pobliżu NPO. Znaleźliśmy dwie wartości czynnika
kontrolującego (
9). Wynika to stąd, że równanie drugiego rzędu
ma dwa liniowo niezależne rozwiązania. Skoncentrujemy sie na przypadku
S ∼ +2 x
−1/2 (x→ 0
+). Drugie rozwiązanie traktuje się
podobnie. Ulepszymy rozwiazanie znajdując funkcję C(x). To znaczy
|
S(x) = 2x−1/2 + C(x) , C(x) << 2 x−1/2 (x→ 0+) . |
| (10) |
Nie możemy spodziewać się, że znajdziemy dokładną funkcję C(x). Byłoby to
równoważne z dokładnym rozwiązaniem równania. Wyznaczymy C(x) tylko
asymptotycznie.
Wstawmy (
10) do oryginalnego równania (
6) z p(x)=0
i q(x)=−x
−3. otrzymamy
[3/2] x
−3/2 + C" − 2 x
−3/2 C′+ (C′)
2 = 0. Równanie to możemy
rozwiązać asymptotycznie korzystając z (
10). Mamy S′ ∼ −x
−3/2 (x→ 0
+) lub równoważnie C′ << x
−3/2 (x→ 0
+). Stąd
(C′)
2 << x
−3/2C′ (x→ 0
+). Prowadzi to do równania asymptotycznego
|
|
3
2
|
x−3/2 + C" ∼ 2 x−3/2 C′ . |
|
Równanie to daje sie rozwiązać, lecz dla treningu uprościmy je jeszcze raz
stosując przybliżenie asymptotyczne. Ponieważ C′ << x
−3/2 (x→0
+)
to różniczkując tę relację (o ile można) dostaniemy
C" << x
−5/2 (x→ 0
+). Stąd
|
|
3
5
|
x−5/2 ∼ 2 x−3/2 C′ , x→ 0+ . |
|
Rozwiązaniem jest więc
Zauważmy, że różniczkowanie (
11) daje C′ ∼ [3/4] x
−2 (x→ 0
+), a więc C" << x
−5/2 (x→ 0
+) tak jak założono.
Wstawiając do (
10) dostaniemy
|
S(x) ∼ 2 x−1/2 + |
3
4
|
lnx + D(x) , |
| (12) |
gdzie D(x) jest funkcją (wynikającą z całkowania relacji asymptotycznej),
która spełnia relację
Spróbujmy znaleźć D(x). Podobnie jak w przypadku funkcji C wstawimy
(
12) do (
6) przy p=0, q=−x
−3. Dostaniemy
|
−3 x−2/16 + D" + (D′)2 − 2 x−3/2 D′+ 3 x−1 D′/2 = 0 . |
|
Biorąc pod uwagę, że x
−1 << x
−3/2 (x→ 0
+), otrzymamy
|
3x−1 D′/2 << 2 x −3/2 D′ , x→ 0+ . |
|
Po drugie D′ << x
−1 (x→ 0
+), co dostajemy różniczkując
(
13), a więc
|
(D′)2 << x−1 D′ , x→ 0+ . |
|
Różniczkując (
13) dwa razy mamy
Na podstawie tych związków, równanie asymptotyczne dla D możemy
zastąpić równaniem
|
−2 x−3/2 D′ ∼ 3 x−2/16 x→ 0+ , |
|
lub
|
D′ ∼ −3 x−1/2/32 , x→ 0+ . |
|
Biorąc całkę nieoznaczoną z obu stron tej relacji, dostaniemy
|
D − d ∼ −3 x1/2/16 , x→ 0+ , |
|
gdzie d jest stałą. Inaczej mówiąc, mamy
gdzie
|
δ(x) ∼ −3x1/2/16 (x→ 0+) . |
|
|
y(x) ∼ exp[ 2 x−1/2 + |
3
4
|
lnx + d] x→ 0+ , |
|
lub
|
y(x) ∼ C1 x3/4 exp(2 x−1/2) (x→ 0+) , |
|
gdzie C1=ed.
Z a d a n i e 2.
Powtórzyć postępowanie dla S(x) ∼ −2 x−1/2 .
Z a d a n i e 3.
Rozwiązać numerycznie równanie x3 y" = y , y(1)=1 , y′(1)=0
na przedziale (0,1). Kładąc eδ(x) = 1+ ϵ(x), gdzie
ϵ→ 0 przy x→ 0+, sprawdzić, że ϵ→ 0 jeśli x→ 0+.
Rozwiązanie równania (1) jest liniową kombinacja rozwiazań,
z których jedno eksponencjalnie maleje przy x→ 0+, a drugie eksponencjalnie
rośnie do ∞.
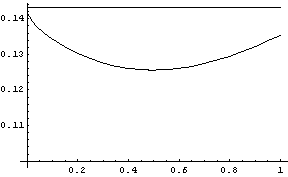
Wykres zależności y(x)/(x
3/4 exp(2 x
−1/2))
gdzie y jest rozwiązaniem równania x
3y" = y [ y(1)=1, y′(1)=0 ].
P r z y k ł a d 3.
Na podstawie wyników poprzedniego zadania wiemy jak zachowuje się wiodący
człon rozwiązania przy x→0
+. Funkcja ϵ(x) zdefiniowana równością
e
δ(x)=1+ϵ(x) dąży do zera. Rozwiązaniem równania x
3y"=y jest
kombinacja liniowa dwu rozwiązań. Jedno z nich rośnie do nieskończoności,
a drugie maleje do zera w granicy x→0
+ (patrz (
2,
3)).
Przy przyjętych warunkach początkowych całkowania numerycznego,
y(0)=1, y′(0)=0, współczynnik przy rozwiązaniu rosnącym jest różny od zera.
Ponieważ rozwiązanie rosnące przewyższa rozwiązanie malejące to jego wkład
dominuje nad składową malejącą w granicy asymptotycznej. Wkład wiodącego
członu
|
y(x)=c1x3/4exp(2x−1/2)[1+ϵ(x)] , |
| (15) |
możemy oszacować, porównując je z rozwiązaniem numerycznym. Aby to zrobić, na
rysunku pokazano funkcję y(x)/(x
3/4exp(2x
−1/2)) w funkcji x
dla 0 < x < 1. Wartość tego stosunku wynosi c
1=0.1432... przy x→0
+.
Odległość pomiędzy tą wartością graniczną i narysowaną krzywą jest proporcjonalna
do funkcji ϵ(x). Rysunek ten ilustruje siłę analizy asymptotycznej.
Pomimo tego, że funkcja y(x) zmienia się o rzędy wielkości, wiodące zachowanie
y(x) jest dobrym przybliżeniem y(x) na całym odcinku 0 ≤ x ≤ 1. Rysunek
pokazuje też, że błąd względny ϵ(x) jest co najwyżej równy 15%. Główne
zachowanie rozwiązania poprawia się dla x→0
+. Widzimy, że oszacowanie funkcji
ϵ(x) może poprawić rozwiązanie.
- Odrzucamy w równaniu wszystkie człony które są małe i zastępujemy równanie
relacją asymptotyczną.
- Zastępujemy relację asymptotyczną równaniem zamieniając
znak ~ znakiem równości = i dokładnie rozwiązujemy tak otrzymane równanie.
Otrzymane rozwiązanie automatycznie spełnia relację asymptotyczną chociaż nie jest to
jedyna spełniająca ją funkcja.
- Sprawdzamy teraz czy otrzymane rozwiązanie jest zgodne z warunkiem
przyjętym w (1). Jeśli zachodzi zgodność to musimy jeszcze pokazać, że równanie
dla funkcji otrzymanej metodą eliminacji rozwiązania dominującego z rozwiązania
dokładnego ma rozwiązanie, które zmienia się wolniej niż rozwiązanie dominujące.
Kiedy tak jest wnioskujemy, że czynnik dominujący jest taki sam jak w rozwiązaniu
dokładnym.
P r z y k ł a d 4.
(c.d.) Poprawki do zachowania głównego w pobliżu początku układu. Wciąż
pozostajemy przy równaniu x
3y"=y. Jego rozwiązanie jest ciągle niepełne gdyż
można znaleźć cały szereg przybliżeń, które je poprawiają w granicy x→0
+.
Znajdziemy kolejne przybliżenia do funkcji ϵ(x) w rozwiązaniu (
15).
Najpierw znajdziemy równanie, które spełnia 1+ϵ(x). Następnie
znajdziemy jego rozwiązanie w postaci formalnego szeregu potęgowego
|
1+ϵ(x) = 1+a1 xα + a2 (xα)2 + a3 (xα)3 + ... , |
| (16) |
gdzie α > 0. Kiedy znajdziemy współczynniki a
k tego szeregu,
rozwiązanie (
1) przy x→0
+ będzie kompletne. Otrzymamy
reprezentację y(x) w postaci szeregu zawierającego funkcje elementarne.
Wstawiając (
16) do (
15) otrzymamy rozwiązanie w postaci
uogólnionego szeregu Frobeniusa. Jest to uogólnienie polegające na tym, że
po pierwsze szereg ten zawiera exponentę która jest istotnie osobliwa. Po
drugie, nie jest to szereg całkowitych potęg x; okaże się, że α = 1/2.
Po trzecie, szereg (
16) jest rozbieżny dla x→0
+. Interpretację tego
faktu odłożymy na później.
Wyliczmy współczynniki a
k, k=1, 2, ... oraz α. Znajdziemy w tym
celu równanie, które spełnia w(x)=1+ϵ(x). Wstawiając (
15)
do (
1) dostaniemy
|
w"+( |
3
2x
|
− |
2
x3/2
|
)w′− |
3
16x2
|
w = 0 . |
| (17) |
Zastąpienie y(x) przez w(x) pozwoliło wydzielić wiodący człon rozwiązania.
Zadanie wydzielenia wiodącego członu jest w analizie asymptotycznej konstrukcja
rozwiązania, które zachowuje sie asymptotycznie jak stała. Nie eliminuje to
z równania NPO.
Z (
2) i (
15) lub na podstawie analizy lokalnej równania
(
17) wynika, że możliwym czynnikiem wiodącym w(x) jest 1 lub
exp(−4x
−1/2).
Zacznijmy obliczenia od znalezienia wiodącego zachowania ϵ(x). W tym celu
wstawmy w(x)=1+ϵ(x) do (
17). Mamy
|
ϵ" + ( |
3
2x
|
− |
2
x3/2
|
)ϵ′− |
3
16x2
|
− |
3ϵ
16x2
|
= 0 . |
|
Zauważmy, że ϵ << 1, x→0
+, a więc
Jednocześnie
Prowadzi to do równania
|
ϵ"− |
2
x3/2
|
ϵ′ ∼ |
3
16x2
|
x→0+ , |
| (18) |
które należy rozwiązać przy warunku ϵ→0, x→0
+.
Zastosujemy metodę dominujacej równowagi. Argumentujemy, że przy x→0
+
dowolny składnik równania (
18) nie może być większy od dwu
pozostałych bez naruszenia warunków, przy których to równanie jest relacją
asymptotyczną. Mamy cztery możliwe przypadki. Rozważymy je w kolejności.
Warunek, który nie prowadzi do sprzeczności to warunek ostatni, ϵ(x) ∼ 3x
1/2/16, x→0
+. Wynik ten poznaliśmy już w (
14).
(a) ϵ" ∼ 3 x−2/16 i 2x−3/2ϵ′ << 3x−2/16,
x→0+. Dwukrotnie całkując pierwszą z relacji, dostaniemy
ϵ ∼ −3lnx/16, x→0+. Jest to sprzeczne z warunkiem
ϵ→0, x→0+.
(b) ϵ"/ϵ′ ∼ 2x−3/2 i 3x−2/16 << 2x−3/2ϵ,
x→0+. Całkowanie pierwszej relacjidaje lnϵ′ ∼ −4x−11/2,
xx→0+. Jest to sprzeczne z założeniem, że 3x−2 << 2x−3/2ϵ′,
x→0+.
(c) Nie można zaniedbać żadnego ze składników w porównaniu z dwoma
pozostałymi.
(d) −2x−3/2ϵ′ ∼ 3x−2/16 i ϵ" << 2x−3/2ϵ,
x→0+. Z pierwszej relacji mamy ϵ ∼ −3x1/2/16.
Pominięta została stała całkowania gdyż ϵ→0 przy x→0+.
Otrzymany wynik nie jest sprzeczny ponieważ ϵ" << 2x−3/2ϵ,
x→0+. Jest to więc jedyny niesprzeczny warunek dominującej równowagi
w tym zagadnieniu.
Pokazaliśmy, że
|
w(x) − 1 ∼ −3x1/2/16 (x→0+) |
|
lub
|
w(x) = 1 − 3x1/2/16 + ϵ1(x) |
|
gdzie ϵ
1(x) << 3x
1/2/16, x→0
+.
Wróćmy do wyników numerycznych (patrz zadanie) pokazanych na poprzednim rysunku.
Zaskoczeniem może się okazać fakt, że nachylenie krzywej ϵ(x) przy
x→0
+ jest pionowe! Wyjaśnia sie to jesli popatrzymy na funkcję 3x
1/2/16,
której nachylenie przy x→0
+ jest nieskończone.
Włączając do rozwiązania wiodący wkład od ϵ(x) otrzymujemy znaczną poprawę
sytuacji. Nowe rozwiązanie asymptotyczne pokazano na następnym rysunku.
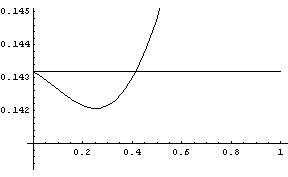
Wykres zależności y(x)/(x
3/4 exp(2 x
−1/2) (1−3/16 x
1/2))
gdzie y jest rozwiązaniem równania x
3y" = y [ y(1)=1, y′(1)=0 ].
Możemy terez znaleźć wiodące zachowanie ϵ
1(x). Postępując podobnie jak
poprzednio otrzymamy
|
ϵ1(x) = −15x/512 + ϵ2(x) , ϵ2 << 15x/512 , x→0+ . |
|
Proces ten można kontynuowac w nieskończoność. Ponieważ jednak formalna struktura
szeregu została odkryta (jest to szereg potęg wielkości x
1/2), mozna postąpić
inaczej. Zapiszemy
|
w(x) = |
∞
∑
n=1
|
an xn/2 , (a0=1) |
|
i wstawmy to bezpośrednio do (
18). Znajdziemy
|
|
∞
∑
n=1
|
|
n
2
|
( |
n
2
|
−1) an xn/2−2+ |
3
2
|
|
∞
∑
n=1
|
an xn/2−2 |
|
|
−2 |
∞
∑
n=1
|
|
n
2
|
an xn/2−5/2− |
3
16
|
|
∞
∑
n=1
|
an xn/2−2 = 0 . |
|
Porównując współczynniki przy jednakowych potęgach dostaniemy rekurencję
|
an+1 = |
(2n−1)(2n+3)
16(n+1)
|
an , n=0,1,2,... |
| (19) |
Mamy więc a
0=1, a
1=−3/16, a
2=−15/512, itd.
Ogólnie
|
an = − |
Γ(n−1/2)Γ(n+3/2)
π4nn!
|
, n=0,1,2,... |
|
Kończy to analizę lokalną rozwiązania równania (
1), którego
wiodącye zachowanie jest postaci
|
y(x) ∼ −c1 x3/4 exp(2x−1/2) |
∞
∑
n=0
|
|
Γ(n−1/2)Γ(n+3/2)
π4nn!
|
xn/2 , x→0+ . |
| (20) |
Można sprawdzić, że promień zbieżności otrzymanego szeregu jest zerowy:
|
R = |
lim
n→∞
|
| ⎢
⎢
|
an
an+1
| ⎢
⎢
|
= |
lim
n→∞
|
| ⎢
⎢
|
16(n+1)
(2n−2)(2n+3)
| ⎢
⎢
|
= 0 . |
|
Szereg (
20) jest rozbieżny dla wszystkich x! Jest to jednakowoż szereg
asymptotyczny i dla x→0
+ będzie on dobrym przybliżeniem y(x).
W podobny sposób dostajemy drugie rozwiazanie rozpatrywanego równania
|
y(x) ∼ −c1 x3/4 exp(2x−12) |
∞
∑
n=0
|
(−1)n |
Γ(n−1/2)Γ(n+3/2)
π4nn!
|
xn/2 , x→0+ . |
| (21) |
P r z y k ł a d 5.
Lokalny przebieg rozwiązań równania Schroedingera n-tego rzędu w pobliżu
nieregularnych punktów osobliwych. Znajdziemy ważny wzór na wiodący przebieg
rozwiązania równania Schroedingera n-tego rzędu
w pobliżu istotnej osobliwości równania x
0.
Podstawienie y(x)=e
S(x) oraz przybliżenie asymptotyczne d
kS/dx
k << (S′)
k,
x→ x
0, k=2,3,..., n, dają asymptotyczne równanie rózniczkowe dla S:
(S′)
n ∼ Q(x), x→ x
0. Stąd S(x) ∼ ω∫
x [Q(t)]
1/ndt,
gdzie ω jest n-tym pierwiastkiem z jedności. Wynik ten wyznacza n
możliwych czynników kontrolnych dla y(x). W zwykły sposób znajdujemy główny
przebieg y(x):
|
y(x) ∼ c [Q(x)](1−n)/2n exp | ⎧
⎨
⎩
|
ω | ⌠
⌡
|
x
|
[Q(t)] dt | ⎫
⎬
⎭
|
, x→ x0 . |
|
Jeśli x
0 ≠ ∞ to (
22) jest słuszne gdy |(x−x
0)
n Q(x)| → ∞
przy x→ x
0. Jeżeli x
0=∞ to (
22) słuszne jest jeśli
|x
n Q(x)| → ∞.
Otrzymany wzór stanowi podstawę metody WKB. Jeżeli Q(x) < 0 to rozwiązanie y(x)
oscyluje przy x→∞.
Z a d a n i e 4.
Pokazać, że asymptotycznymi rozwiązaniami podanych równań są funkcje
wypisane obok tych równań.
(a) y"=y/x5; y(x) ∼ cx5/4exp(±2x−3/2/3) , (x→0+).
(b) y"=xy; y(x) ∼ cx−1/3exp(3ωx4/3/3) , (x→∞) , ω3=1.
(c) y(iv)=(x4+sinx) y; y(x) ∼ cx−3/2exp(ωx2/2) , (x→∞) , ω = ±1,±i.
File translated from
TEX
by
TTH,
version 4.08.
On 23 Dec 2015, 13:49.



