Podstawa: F. Bowman; prawie dosłowny przekład §61-§63

1  Funkcja Gamma Γ(n) Eulera

Funkcja Γ(n) odgrywa ważną rolę w teorii funkcji specjalnych. Przypomnimy jej definicję i podstawowe własności.

1.1  Definicja całkowa

Kiedy n jest dodatnie i całkowite funkcja Γ jest zdefiniowana całką:
Γ(n) = ⌠
⌡ 		∞

0 
 e−xxn−1 dx ,    (n > 0)
(1)
Warunek n > 0 zapewnia zbieżność całki w x=0. Całkując przez części mamy
Γ(n) = [−e−xxn−1]0∞ + (n−1)⌠
⌡ 		∞

0 
 e−xxn−2dx ,
(2)
a więc
Γ(n) = (n−1)Γ(n−1) ,
(3)
lub
Γ(n+1) = n Γ(n) = n(n−1)(n−2) ... 3 ·2·1 Γ(1) .
(4)
Ponieważ
Γ(1) = ⌠
⌡ 		∞

0 
 e−xdx = 1 ,
(5)
więc mamy
Γ(n+1) = n! .
(6)
Wstawiając w (1) x → x2 mamy również
Γ(n) = 2⌠
⌡ 		∞

0 
 e−x2x2n−1 dx .
(7)
Całka
⌠
⌡ 		π/2

0 
 cosmθsinnθ
(8)
daje się przedstawić za pomocą funkcji Gamma. W tym celu wyliczymy na dwa sposoby całkę podwójną
u = ⌠
⌡ 		∞

0 
 ⌠
⌡ 		∞

0 
 e−x2−y2x2m−1y2n−1 dx dy  .
(9)
Z równania (7) mamy
u = ⌠
⌡ 		∞

0 
 e−x2x2m−1 ⌠
⌡ 		∞

0 
 e−y2y2n−1 = 1
4
 Γ(m)Γ(n) .
(10)
Z drugiej strony, po przejściu do współrzędnych biegunowych
u
= ⌠
⌡ 		π/2

0 
 e−r2 (r cosθ)2m−1 (r sinθ)2n−1
= ⌠
⌡ 		∞

0 
 e−r2 r2m+2n−1dr ⌠
⌡ 		π/2

0 
 cos2m−1θsin2n−1θ dθ ,
co wynika z (7). Porównując oba wyniki mamy
⌠
⌡ 		π/2

0 
 cos2m−1θ sin2n−1θ dθ = Γ(m)Γ(n)
2Γ(m+n)
  .
(11)
Wynika stąd, że dla m > −1, n > −1
⌠
⌡ 		π/2

0 
 cosmθ sinnθ dθ = Γ((m+1)/2)Γ((n+1)/2)
2Γ((m+n)/2)
  .
(12)
W szczególności dla m=0, n=0, mamy
π
2
 = ⌠
⌡ 		π/2

0 
 dθ = Γ(1/2)2
2Γ(1)
 =Γ(1/2)2/2 .
(13)
Z równania (3) mamy w szczególności
Γ(3/2)
=
Γ(1/2)/2 = 1
2
 √2 ,
Γ(7/2)
=
3
2
 Γ(3/2) = 1·3
22
√
 
π
 
  ,
Γ(5/2)
=
5
2
 Γ(5/2) = 1·3·5
23
√
 
π
 
  ,
itd. Z równania (4)
Γ(n) = Γ(n+1)
n
  .
(14)
Stąd wynika, że Γ(n)→+∞ jeśli n→+0. Załóżmy teraz, że (14) jest spełnione dla −1 ≤ n ≤ 0, następnie dla −2 ≤ n ≤ −1, dalej dla −3 ≤ n ≤ −2 itd. W ten sposób funkcja Gamma została zdefiniowana dla wszystkich rzeczywistych wartości n. Np. z (14) i (13) mamy
Γ(− 1
2
 ) = Γ(1/2)
−1/2
 = −2
√
 
π
 
  ,

Γ(− 3
2
 ) = Γ(1/2)
−3/2
 = 22
1·3
  ,
(15)
itd. Oprócz definicji Γ danej równaniem (1) można podać inne definicje równoważne.

1.2  Formuła graniczna Eulera

Tzw. wzorem granicznym dla Γ(z) jest wyrażenie
Γ(z)=
lim
n→∞ 
 n!zn
z(z+1)...(z+n)
(16)
Pokażemy jak otrzymać formułę graniczną. Wychodzimy z formuły całkowej Eulera.
Γ(z) = ⌠
⌡ 		∞

0 
 e−xxz−1 dx =
lim
n→∞ 
 ⌠
⌡ 		∞

0 
 (1−x/n)nzz−1 dx
(17)
Przejdziemy do nowej zmiennej u=x/n i otrzymaną całkę obliczymy przez części
⌠
⌡ 		1

0 
 (1−u)n(n u)z−1n du = nz⎡
⎣ 		uz
z
 (1−u)n|01 + n
z
 ⌠
⌡ 		1

0 
 (1−u)n−1uz du ⎤
⎦ 		 .
(18)
Pierwsza składowa znika. Kontynuując obliczenia przez części dostajemy
⌠
⌡ 		1

0 
 (1−u)n(n u)z−1n du = nzn(n−1)...(1)
z(z+1)...(z+n−1)
 ⌠
⌡ 		1

0 
 uz+n−1 du
(19)
Stąd, składając mamy formułę graniczną (16). Formuła graniczna pokazuje, że tak zdefiniowana funkcja Γ(z) jest określona wszędzie w płaszczyźnie zespolonej z wyjątkiem punktów z=0, −1, −2, gdzie funkcja posiada proste bieguny.

1.3  Formuła Weierstrassa

Wzór albo formuła Weierstrasa podaje jeszcze inną postać Γ
1
Γ(z)
 =ezγ
lim
n→∞ 
 n
∏
s=1 
 ⎛
⎝ 		1+ z
s
⎞
⎠ 		ezś ,
(20)
gdzie γ jest stałą Eulera-Mascheroni
γ =
lim
n→∞ 
 ⎡
⎣ 		1+ 1
2
 + 1
3
 +...+ 1
n
 −lnn ⎤
⎦ 		≈ 0.5772156649.
(21)
Aby pokazać słuszność wzoru Weierstrassa (20) zauważmy, że
1·2...·n
(z+1)(z+2)...(z+n)
 = n
∏
s=1 
 ⎛
⎝ 		s
s+z
⎞
⎠ 		= n
∏
s=1 
 ⎛
⎝ 		s+z
s
⎞
⎠ 		−1

 
  .
(22)
Odwracając graniczny wzór Eulera można więc napisać
1
Γ(z)
 =
lim
n→∞ 
 z n
∏
s=1 
 ⎛
⎝ 		1+ z
s
⎞
⎠ 		n−z .
(23)
Zapisując n−z=e−zlnn, mnożąc i dzieląc przez
exp⎡
⎣ 		(1+ 1
2
 + 1
3
 + ... + 1
n
 )z⎤
⎦ 		= n
∏
s=1 
 e−z/s ,
(24)
dostaniemy
1
Γ(z)
 =z⎧
⎨
⎩
lim
n→∞ 
 exp⎡
⎣ 		(1+ 1
2
 + 1
3
 + ... + 1
n
 − lnn)z⎤
⎦ 		⎫
⎬
⎭ 		⎧
⎨
⎩
lim
n→∞ 
 n
∏
s=1 
 ⎛
⎝ 		1+ z
s
⎞
⎠ 		−z/s

 
⎫
⎬
⎭ 		 .
(25)
Pierwszy czynnik {...} jest równy stałej γ. Otrzymaliśmy więc wzór (20).

1.4  Wzór Stirlinga

Przytoczymy bez dowodu asymptotyczny szereg Stirlinga dla Γ.
ln(z!) = 1
2
 ln2π+(z+ 1
2
 lnz + 1
12 z
 − 1
360 z3
 + 1
1260 z5
 + ...)
(26)
Tutaj z! = Γ(z+1). Szereg Stirlinga wraz z formułami redukcyjną i odbiciową jest wygodny do obliczeń Γ dla dowolnych z.

1.5  Zadania

Z a d a n i e 1.  Oblicz residua funkcji Γ w punktach 0, -1, -2, ...

Z a d a n i e 2.  Otrzymać wzór podwajania √{π} Γ(2x)=22x−1Γ(x)Γ(x+1/2) oraz wzór odbiciowy Γ(x)Γ(1−x)=π/sin(πx).

Z a d a n i e 3.  Mając Γ(1/4) ≈ 3.62561 i Γ(1/3) ≈ 2.67894 wyznaczyć Γ(2/3), Γ(3/4), Γ(1/6), Γ(5/6).

Z a d a n i e 4.  Napisać program, który oblicza Γ(n) dla dowolnego, rzeczywistego n. W przypadku niepowodzenia(!) wykorzystać wyniki poprzedniego zadania lub następującą tablicę zawierającą kilka wartości funkcji Γ(n) dla n z przedziału [1, 2].1

n Γ
1 00 1.00000 00000
1.25 0.90640 24771
1.50 0.88622 69255
1.75 0.91906 25268
2.00 1.00000 00000
Sprawdź dokładność obliczeń. Jak zwiększyć dokładność?

Z a d a n i e 5.  Sporządzić grafik Γ(n) dla n ∈ [−4,4]. Wynik powinien przypominać grafik pokazany poniżej.

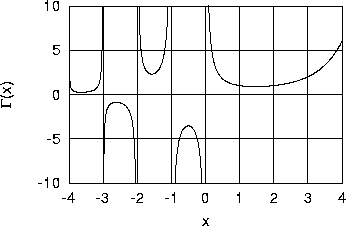
pict/gamma.gif
Funkcja Γ(n). Rysunek wykonano programem gnuplot.

Z a d a n i e 6.  Porównać napisany program numeryczny z moim, gdzie wykorzystano przybliżenie Hastingsa Γ(x+1)=1+∑18 bnxn. Współczynniki bn , n=1,...,8 podane zostały w programie (patrz również Arfken). Wartości Γ dla ujemnych argumentów obliczane są z formuły odbiciowej. Dla dużych x zastosowano szereg Stirlinga.

Z a d a n i e 7.  Napisz program obliczający Γ(z) z szeregu Stirlinga (dla dowolnych z). Porównaj wyniki z wynikami otrzymanymi z poprzednich programów. U w a g a: W celu osiągnięcia dobrej dokładności obliczeń ...

Footnotes:

1Co wiesz o aproksymacji wielomianowej?

File translated from TEX by TTH, version 4.08.
On 23 Dec 2015, 13:48.